Fundamentals of Heat and Mass Transfer
7th Edition
ISBN: 9780470917855
Author: Bergman, Theodore L./
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 4, Problem 4.61P
The steady-state temperatures (°C) associated with selected nodal points of a two-dimensional system having a thermal conductivity of 1.5 are shown on the accompanying grid.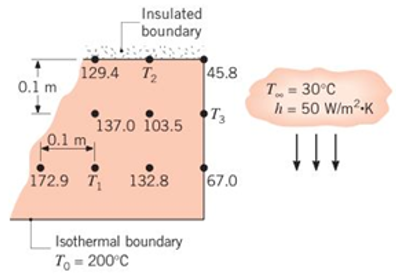 
- Determine the temperatures at nodes 1, 2, and 3.
- Calculate the heat transfer rate per unit thickness normal to the page from the system to the fluid.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Hi, kindly help me with this and show the complete solution. Thank you
Hi, kindly solve this problem and show the solution. Thank you
Do part 3,4
Chapter 4 Solutions
Fundamentals of Heat and Mass Transfer
Ch. 4 - In the method of separation of variables (Section...Ch. 4 - A two-dimensional rectangular plate is subjected...Ch. 4 - Consider the two-dimensional rectangular plate of...Ch. 4 - A two-dimensional rectangular plate is subjected...Ch. 4 - A two-dimensional rectangular plate is subjected...Ch. 4 - Using the thermal resistance relations developed...Ch. 4 - Free convection heat transfer is sometimes...Ch. 4 - Consider Problem 4.5 for the case where the plate...Ch. 4 - Prob. 4.9PCh. 4 - Based on the dimensionless conduction heat rates...
Ch. 4 - Determine the heat transfer rate between two...Ch. 4 - A two-dimensional object is subjected to...Ch. 4 - An electrical heater 100 mm long and 5 mm in...Ch. 4 - Two parallel pipelines spaced 0.5 m apart are...Ch. 4 - A small water droplet of diameter D=100m and...Ch. 4 - A tube of diameter 50 mm having a surface...Ch. 4 - Pressurized steam at 450K flows through a long,...Ch. 4 - The temperature distribution in laser-irradiated...Ch. 4 - Hot water at 85°C flows through a thin-walled...Ch. 4 - A furnace of cubical shape, with external...Ch. 4 - Laser beams are used to thermally process...Ch. 4 - A double-glazed window consists of two sheets of...Ch. 4 - A pipeline, used for the transport of crude oil,...Ch. 4 - A long power transmission cable is buried at a...Ch. 4 - A small device is used to measure the surface...Ch. 4 - A cubical glass melting furnace has exterior...Ch. 4 - An aluminum heat sink (k=240W/mK), used to cool an...Ch. 4 - Hot water is transported from a cogeneration power...Ch. 4 - A long constantan wire of 1-mm diameter is butt...Ch. 4 - A hole of diameter D=0.25m is drilled through the...Ch. 4 - In Chapter 3 we that, whenever fins are attached...Ch. 4 - An igloo is built in the shape of a hemisphere,...Ch. 4 - Prob. 4.34PCh. 4 - An electronic device, in the form of a disk 20 mm...Ch. 4 - The elemental unit of an air heater consists of a...Ch. 4 - Prob. 4.37PCh. 4 - Prob. 4.38PCh. 4 - Prob. 4.39PCh. 4 - Prob. 4.40PCh. 4 - One of the strengths of numerical methods is their...Ch. 4 - Determine expressionsfor...Ch. 4 - Consider heat transfer in a one-dimensional...Ch. 4 - In a two-dimensional cylindrical configuration,...Ch. 4 - Upper and lower surfaces of a bus bar are...Ch. 4 - Derive the nodal finite-difference equations for...Ch. 4 - Consider the nodal point 0 located on the boundary...Ch. 4 - Prob. 4.48PCh. 4 - Prob. 4.49PCh. 4 - Consider the network for a two-dimensional system...Ch. 4 - An ancient myth describes how a wooden ship was...Ch. 4 - Consider the square channel shown in the sketch...Ch. 4 - A long conducting rod of rectangular cross section...Ch. 4 - A flue passing hot exhaust gases has a square...Ch. 4 - Steady-state temperatures (K) at three nodal...Ch. 4 - Functionally graded materials are intentionally...Ch. 4 - Steady-state temperatures at selected nodal points...Ch. 4 - Consider an aluminum heat sink (k=240W/mK), such...Ch. 4 - Conduction within relatively complex geometries...Ch. 4 - Prob. 4.60PCh. 4 - The steady-state temperatures (°C) associated with...Ch. 4 - A steady-state, finite-difference analysis has...Ch. 4 - Prob. 4.63PCh. 4 - Prob. 4.64PCh. 4 - Consider a two-dimensional. straight triangular...Ch. 4 - A common arrangement for heating a large surface...Ch. 4 - A long, solid cylinder of diameter D=25mm is...Ch. 4 - Consider Problem 4.69. An engineer desires to...Ch. 4 - Prob. 4.71PCh. 4 - Prob. 4.72PCh. 4 - Prob. 4.73PCh. 4 - Refer to the two-dimensional rectangular plate of...Ch. 4 - The shape factor for conduction through the edge...Ch. 4 - Prob. 4.77PCh. 4 - A simplified representation for cooling in very...Ch. 4 - Prob. 4.84PCh. 4 - A long trapezoidal bar is subjected to uniform...Ch. 4 - Consider the system of Problem 4.54. The interior...Ch. 4 - A long furnace. constructed from refractory brick...Ch. 4 - A hot pipe is embedded eccentrically as shown in a...Ch. 4 - A hot liquid flows along a V-groove in a solid...Ch. 4 - Prob. 4S.5PCh. 4 - Hollow prismatic bars fabricated from plain carbon...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- 1.3 A furnace wall is to be constructed of brick having standard dimensions of Two kinds of material are available. One has a maximum usable temperature of 1040°C and a thermal conductivity of 1.7 W/(m K), and the other has a maximum temperature limit of 870°C and a thermal conductivity of 0.85 W/(m K). The bricks have the same cost and are laid in any manner, but we wish to design the most economical wall for a furnace with a temperature of 1040°C on the hot side and 200°C on the cold side. If the maximum amount of heat transfer permissible is 950 , determine the most economical arrangement using the available bricks.arrow_forwardIn the design of a certain computer application, a heat flow simulation is required. In the simulation, the heat conductor, which is of length 10m, has a perfectly insulated surface. The temperature at both ends of the conductor is kept consistently at zero. The initial temperature at any point of the conductor is uniform at 25°C. The 1-dimensional heat equation is given as follows: for all 0arrow_forwardShow detailed step by step solution. Topic: Thermodynamicsarrow_forwardQ4/ A room on the second floor of a house with a balcony has a door. The door made of teak (wood) and it contains a large sheet of glass (outside winter type) in the middle and constitutes 80% of the area of the door. Door thickness is 40 mm and the temperature in the room 25. °C when the temperature is in the balcony 8 °C. Calculate the rate of heat loss from the room to the balcony through the door. The door dimensions 2m x 1m. Assume Inside and outside still air thermal resistance f= 8.29 W/m2 °C and f. 34.1 W/m2 °C respectivelyarrow_forwardPlease solve the question on the sheet and get a clear picture and submit the picture. thankyouarrow_forwardTo find the thermal conductivity of a material, the following experimental setup can be prepared. Two long cylinders that are identical in terms of manufacturing are prepared. One of them is of a known thermal conductivity value kA while the other is for an unknown material kB. Both cylinders are attached to a heat sink of a fixed temperature Tb and they are exposed to a fluid (typically ultra-cooled for accuracy purposes). The temperature measurements are taken along some distance (x1) away from the base. If the first measurements reads 65 C for a distance (x1) of 12 mm while the second material reads 54 C for the same distance. What is the thermal conductivity of the second material (B).Knowns: material A is made of copper. k = 390 W/m.k. Tb = 130 C, Tinf = 12 C.arrow_forwardCompletely solve and box the final answers. Write legiblyarrow_forwardHello sir Can you solve this problem because i did'nt understand about subject (heat transfer)arrow_forward8m long rod is at an initial temperature of 80c the left side of the rod is at temperature equal to 39c and the right side is at temperature equal to 68c thermal diffusivity is equal to 10^-4 and grid space is equal to 2m find the temperature distribution at 30_60_90 secondsarrow_forwardA 1-D conduction heat transfer problem with internal energy generation is governed by the following equation: +-= dx2 =0 W where è = 5E5 and k = 32 If you are given the following node diagram with a spacing of Ax = .02m and know that m-K T = 611K and T, = 600K, write the general equation for these internal nodes in finite difference form and determine the temperature at nodes 3 and 4. Insulated Ar , T For the answer window, enter the temperature at node 4 in Kelvin (K). Your Answer: EN SORN Answer units Pri qu) 232 PM 4/27/2022 99+ 66°F Sunny a . 20 ENLARGED oW TEXTURE PRT SCR IOS DEL F8 F10 F12 BACKSPACE num - %3D LOCK HOME PGUP 170arrow_forwardsolve this question completlyarrow_forwardConsider the square channel shown in the sketch operating under steady state condition. The inner surface of the channel is at a uniform temperature of 600 K and the outer surface is at a uniform temperature of 300 K. From a symmetrical elemental of the channel, a two-dimensional grid has been constructed as in the right figure below. The points are spaced by equal distance. Tout = 300 K k = 1 W/m-K T = 600 K (a) The heat transfer from inside to outside is only by conduction across the channel wall. Beginning with properly defined control volumes, derive the finite difference equations for locations 123. You can also use (n, m) to represent row and column. For example, location Dis (3, 3), location is (3,1), and location 3 is (3,5). (hint: I have already put a control volume around this locations with dashed boarder.) (b) Please use excel to construct the tables of temperatures and finite difference. Solve for the temperatures of each locations. Print out the tables in the spread…arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Understanding Conduction and the Heat Equation; Author: The Efficient Engineer;https://www.youtube.com/watch?v=6jQsLAqrZGQ;License: Standard youtube license