Chapter 4, Problem 4.57P

Steady-state temperatures at selected nodal points of the symmetrical section of a flow channel are known to be $T_2=95.47°\text{C,}{T}_3=117.3°\text{C,}{T}_5=79.79°\text{C,}\text{}{T}_6=77.29°\text{C,}{T}_8=87.28°\text{C,}$ and $T_{10}=77.65°\text{C}\text{.}$ The wall experiences uniform volumetric heat generation of $\stackrel{.}{q}={10}^6{\text{W/m}}^{\text{3}}$ and has a thermal conductivity of $k=10\text{W/m}\text{}\cdot \text{K}\text{.}$ The inner and outer surfaces of the channel experience convection with fluid temperatures of $T_{\infty ,i}=50°\text{C}$ and $T_{\infty ,o}=25°\text{C}$ and convection coefficients of $h_i=500{\text{W/m}}^{\text{2}}\cdot \text{K}$ and $h_o=250{\text{W/m}}^{\text{2}}\cdot \text{K}\text{.}$

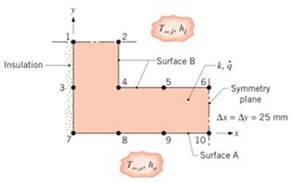
1. Determine the temperatures at nodes 1, 4, 7, and 9.
2. Calculate the heat rate per unit length (W/m) from the outer surface A to the adjacent fluid.
3. Calculate the heat rate per unit length from the inner fluid to surface B.
4. Verify that your results are consistent with an over-all energy balance on the channel section.