
Fundamentals of Heat and Mass Transfer
7th Edition
ISBN: 9780470917855
Author: Bergman, Theodore L./
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 4, Problem 4.41P
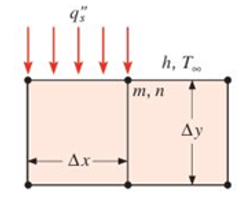
One of the strengths of numerical methods is their ability to handle complex boundary conditions. In the sketch, the boundary condition changes from specified heat flux
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Draw a rough graph & estimate the results just need an idea in very short time plz.
2. As shown in the right figure, write out your
solution strategy, including model, meshing(at least
2Nim
with 4 elements), boundary conditions, and
element type and shape functions, also write out
the nodal force
formula. Do not require
computing.
2Nim
2m
2m
SOLVE IN DIGITAL FORMAT
Chapter 4 Solutions
Fundamentals of Heat and Mass Transfer
Ch. 4 - In the method of separation of variables (Section...Ch. 4 - A two-dimensional rectangular plate is subjected...Ch. 4 - Consider the two-dimensional rectangular plate of...Ch. 4 - A two-dimensional rectangular plate is subjected...Ch. 4 - A two-dimensional rectangular plate is subjected...Ch. 4 - Using the thermal resistance relations developed...Ch. 4 - Free convection heat transfer is sometimes...Ch. 4 - Consider Problem 4.5 for the case where the plate...Ch. 4 - Prob. 4.9PCh. 4 - Based on the dimensionless conduction heat rates...
Ch. 4 - Determine the heat transfer rate between two...Ch. 4 - A two-dimensional object is subjected to...Ch. 4 - An electrical heater 100 mm long and 5 mm in...Ch. 4 - Two parallel pipelines spaced 0.5 m apart are...Ch. 4 - A small water droplet of diameter D=100m and...Ch. 4 - A tube of diameter 50 mm having a surface...Ch. 4 - Pressurized steam at 450K flows through a long,...Ch. 4 - The temperature distribution in laser-irradiated...Ch. 4 - Hot water at 85°C flows through a thin-walled...Ch. 4 - A furnace of cubical shape, with external...Ch. 4 - Laser beams are used to thermally process...Ch. 4 - A double-glazed window consists of two sheets of...Ch. 4 - A pipeline, used for the transport of crude oil,...Ch. 4 - A long power transmission cable is buried at a...Ch. 4 - A small device is used to measure the surface...Ch. 4 - A cubical glass melting furnace has exterior...Ch. 4 - An aluminum heat sink (k=240W/mK), used to cool an...Ch. 4 - Hot water is transported from a cogeneration power...Ch. 4 - A long constantan wire of 1-mm diameter is butt...Ch. 4 - A hole of diameter D=0.25m is drilled through the...Ch. 4 - In Chapter 3 we that, whenever fins are attached...Ch. 4 - An igloo is built in the shape of a hemisphere,...Ch. 4 - Prob. 4.34PCh. 4 - An electronic device, in the form of a disk 20 mm...Ch. 4 - The elemental unit of an air heater consists of a...Ch. 4 - Prob. 4.37PCh. 4 - Prob. 4.38PCh. 4 - Prob. 4.39PCh. 4 - Prob. 4.40PCh. 4 - One of the strengths of numerical methods is their...Ch. 4 - Determine expressionsfor...Ch. 4 - Consider heat transfer in a one-dimensional...Ch. 4 - In a two-dimensional cylindrical configuration,...Ch. 4 - Upper and lower surfaces of a bus bar are...Ch. 4 - Derive the nodal finite-difference equations for...Ch. 4 - Consider the nodal point 0 located on the boundary...Ch. 4 - Prob. 4.48PCh. 4 - Prob. 4.49PCh. 4 - Consider the network for a two-dimensional system...Ch. 4 - An ancient myth describes how a wooden ship was...Ch. 4 - Consider the square channel shown in the sketch...Ch. 4 - A long conducting rod of rectangular cross section...Ch. 4 - A flue passing hot exhaust gases has a square...Ch. 4 - Steady-state temperatures (K) at three nodal...Ch. 4 - Functionally graded materials are intentionally...Ch. 4 - Steady-state temperatures at selected nodal points...Ch. 4 - Consider an aluminum heat sink (k=240W/mK), such...Ch. 4 - Conduction within relatively complex geometries...Ch. 4 - Prob. 4.60PCh. 4 - The steady-state temperatures (°C) associated with...Ch. 4 - A steady-state, finite-difference analysis has...Ch. 4 - Prob. 4.63PCh. 4 - Prob. 4.64PCh. 4 - Consider a two-dimensional. straight triangular...Ch. 4 - A common arrangement for heating a large surface...Ch. 4 - A long, solid cylinder of diameter D=25mm is...Ch. 4 - Consider Problem 4.69. An engineer desires to...Ch. 4 - Prob. 4.71PCh. 4 - Prob. 4.72PCh. 4 - Prob. 4.73PCh. 4 - Refer to the two-dimensional rectangular plate of...Ch. 4 - The shape factor for conduction through the edge...Ch. 4 - Prob. 4.77PCh. 4 - A simplified representation for cooling in very...Ch. 4 - Prob. 4.84PCh. 4 - A long trapezoidal bar is subjected to uniform...Ch. 4 - Consider the system of Problem 4.54. The interior...Ch. 4 - A long furnace. constructed from refractory brick...Ch. 4 - A hot pipe is embedded eccentrically as shown in a...Ch. 4 - A hot liquid flows along a V-groove in a solid...Ch. 4 - Prob. 4S.5PCh. 4 - Hollow prismatic bars fabricated from plain carbon...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Explain the term ‘shape function’. Why polynomial terms are preferred for shape functions in finite element method? Note: Please I need soultion without palagrism and not handwritearrow_forward(3) For the given boundary value problem, the exact solution is given as = 3x - 7y. (a) Based on the exact solution, find the values on all sides, (b) discretize the domain into 16 elements and 15 evenly spaced nodes. Run poisson.m and check if the finite element approximation and exact solution matches, (c) plot the D values from step (b) using topo.m. y Side 3 Side 1 8.0 (4) The temperature distribution in a flat slab needs to be studied under the conditions shown i the table. The ? in table indicates insulated boundary and Q is the distributed heat source. I all cases assume the upper and lower boundaries are insulated. Assume that the units of length energy, and temperature for the values shown are consistent with a unit value for the coefficier of thermal conductivity. Boundary Temperatures 6 Case A C D. D. 00 LEGION Side 4 z episarrow_forwardLet's assume that the outdoor temperature in your region was 1 C on 26.12.2002. Let's assume that you use a 2088 W heater in the room in order to keep the indoor temperature of the room at 20 ° C. In the meantime, a 68 W light bulb for lighting, a computer you use to solve this question and load it into the system (let's assume it consumes 217 W of energy), you and your two friends (three people in total) are in the room to assist you in solving the questions. A person radiates 45 J of heat per second to his environment. When you consider all these conditions, calculate the exergy destruction caused by the heat loss from the exterior wall of your room.arrow_forward
- One of the strengths of numerical methods is their ability to handle complex boundary conditions. In the sketch, the boundary condition changes from specified heat flux ′′ qs (into the domain) to convection, at the location of the node (m, n). Write the steady-state, two- dimensional finite difference equation at this node.arrow_forwardConsider a wall of thickness 50 mm and thermal conductivity 14 W/m.K, the left side (x-0) is insulated. Heat generation (q) is present within the wall and the one dimensional steady-state temperature distribution is given by T(x) = ax +bxtc [°C] , where c 200 °C, a = -1285 °C/m , b=needs to he determined, andx is in meters. What is the heat fluxes at the right side, x = L, (kW/m )? 9, K 4L) Insulationarrow_forwardThis is a multiple-part question, I just need help with part C, Table 2.2 is provided and you can refer to above parts for equations and boundary equations.arrow_forward
- The exercise concerns the Gauss-Legendre integration method for integrals of the form that is in the picture i uploaded with the difference that the integration will not be done at the N+1 specific points (or Gauss nodes: x_0, x_1, …, x_N) as tabulated in your book, but at N+1 points placed arbitrarily (but in monotonically increasing order) in the interval [-1, 1]. If f(x) is a polynomial of degree K, what is the largest value of K (expressed, obviously, as a function of N) for which the integral I is calculated exactly. Provide a convincing numerical demonstration of your answer for N=3 (choosing your own values for x_0, x_1, x_2, x_3).arrow_forwardThe Laws of Physics are written for a Lagrangian system, a well-defined system which we follow around – we will refer to this as a control system (CSys). For our engineering problems we are more interested in an Eulerian system where we have a fixed control volume, CV, (like a pipe or a room) and matter can flow into or out of the CV. We previously derived the material or substantial derivative which is the differential transformation for properties which are functions of x,y,z, t. We now introduce the Reynold’s Transport Theorem (RTT) which gives the transformation for a macroscopic finite size CV. At any instant in time the material inside a control volume can be identified as a control System and we could then follow this System as it leaves the control volume and flows along streamlines by a Lagrangian analysis. RTT:DBsys/Dt = ∂/∂t ʃCV (ρb dVol) + ʃCS ρbV•n dA; uses the RTT to apply the laws for conservation of mass, momentum (Newton's Law), and energy (1st Law of…arrow_forwardThe Laws of Physics are written for a Lagrangian system, a well-defined system which we follow around – we will refer to this as a control system (CSys). For our engineering problems we are more interested in an Eulerian system where we have a fixed control volume, CV, (like a pipe or a room) and matter can flow into or out of the CV. We previously derived the material or substantial derivative which is the differential transformation for properties which are functions of x,y,z, t. We now introduce the Reynold’s Transport Theorem (RTT) which gives the transformation for a macroscopic finite size CV. At any instant in time the material inside a control volume can be identified as a control System and we could then follow this System as it leaves the control volume and flows along streamlines by a Lagrangian analysis. RTT:DBsys/Dt = ∂/∂t ʃCV (ρb dVol) + ʃCS ρbV•n dA; uses the RTT to apply the laws for conservation of mass, momentum (Newton's Law), and energy (1st Law of…arrow_forward
- The Laws of Physics are written for a Lagrangian system, a well-defined system which we follow around – we will refer to this as a control system (CSys). For our engineering problems we are more interested in an Eulerian system where we have a fixed control volume, CV, (like a pipe or a room) and matter can flow into or out of the CV. We previously derived the material or substantial derivative which is the differential transformation for properties which are functions of x,y,z, t. We now introduce the Reynold’s Transport Theorem (RTT) which gives the transformation for a macroscopic finite size CV. At any instant in time the material inside a control volume can be identified as a control System and we could then follow this System as it leaves the control volume and flows along streamlines by a Lagrangian analysis. RTT:DBsys/Dt = ∂/∂t ʃCV (ρb dVol) + ʃCS ρbV•n dA; uses the RTT to apply the laws for conservation of mass, momentum (Newton's Law), and energy (1st Law of…arrow_forwardCircle final answer Question: Which series helps us to derive the discretized form of the governing equations? Remember to circle final answerarrow_forwardPlease don't provide handwritten solution ....arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning

Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Heat Transfer – Conduction, Convection and Radiation; Author: NG Science;https://www.youtube.com/watch?v=Me60Ti0E_rY;License: Standard youtube license