
Fundamentals of Heat and Mass Transfer
7th Edition
ISBN: 9780470917855
Author: Bergman, Theodore L./
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 4, Problem 4.55P
Steady-state temperatures (K) at three nodal points of a long rectangular rod are as shown. The rod experiences a uniform volumetric generation rate of
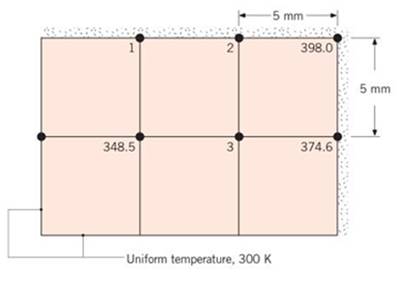
- Determine the temperatures at nodes 1, 2, and 3.
- Calculate the heat transfer rate per unit length (W/rn) from the rod using the nodal temperatures. Compare this result with the heat rate calculated from knowledge of the volumetric generation rate and the rod dimensions.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Battery operated train
Mueh
Groll
CD Af Pair
160,000 kg 0.0005
0.15
19
5m² 1.2kg/m³ 0.98 0.9
Tet neng
0.88
Tesla Prated
Tesla Trated Ywheel ng
Joyle
2
270 kW
440NM
0,45m 20
8.5kg m
Consider a drive cycle of a 500km trip with 3 stops in
the middle. Other than the acceleration and deceleration
associated with the three stops, the tran maintains.
constant cruise speed velocity of 324 km/hr. The
tran will fast charge at each stop for 15 min at a
rate Peharge = 350 kW
Εμ
(MN
15MIN
Stop
w charging
(350kW)
GMIJ
t
6MM
6AW
1) calculate the battery power required to mantain.
constant velocity
of
324km/hr
2) determine the battery energy,
energy required to
constant velocity portion of this drive.
Cover the
3) calculate the battery energy required to accelerate
the train to 324/04/hr.
4) calculate the battery energy that is either fost
in deceleration or recovered due to regenerative
breaking
etc
A 22-lb block B rests as shown on a 28-lb bracket A. The coefficients of friction are μs=0.30μs=0.30 and μk=0.25μk=0.25 between block B and bracket A, and there is no friction in the pulley or between the bracket and the horizontal surface. solved in a previous part. max weight of block C if block B is not to slide on bracket A is 5.045 lbs. Please solve for the acceleration of each Block
Test 1 .DOCX * A
File Edit View
Tools Help
INDUSTRIAL ENGINEERING PROGRAMME
IMB 411-INDUSTRIAL LOGISTICS
TEST 1- SEPTEMBER 12, 2012
Instructions: Answer all questions. Time allowed is 1.5 hours. Identify your script with your
student number ONLY (Do not write your name).
1. Define the following terms
(i) Logistics management
(ii) Supply chain management
(iii) Vertical integration in a supply chain
(3 Marks)
(3 Marks)
(3 Marks)
2. (a) Using examples of your choice, briefly discuss the following levels of customer
service
(1) Pre-transaction elements
(ii) Transaction elements
(4 Marks)
(4 Marks)
(iii) Post-transaction elements
(4 Marks)
(b) "The challenge facing Dumelang Enterprise (Pty) Ltd is to establish the real
profitability of their customers and to develop service strategies that will improve the
profitability of all customers". As a logistics consultant, briefly discuss how you can
advise Dumelang's customer service management.
3. (a) List the three main forms of inventory in a…
Chapter 4 Solutions
Fundamentals of Heat and Mass Transfer
Ch. 4 - In the method of separation of variables (Section...Ch. 4 - A two-dimensional rectangular plate is subjected...Ch. 4 - Consider the two-dimensional rectangular plate of...Ch. 4 - A two-dimensional rectangular plate is subjected...Ch. 4 - A two-dimensional rectangular plate is subjected...Ch. 4 - Using the thermal resistance relations developed...Ch. 4 - Free convection heat transfer is sometimes...Ch. 4 - Consider Problem 4.5 for the case where the plate...Ch. 4 - Prob. 4.9PCh. 4 - Based on the dimensionless conduction heat rates...
Ch. 4 - Determine the heat transfer rate between two...Ch. 4 - A two-dimensional object is subjected to...Ch. 4 - An electrical heater 100 mm long and 5 mm in...Ch. 4 - Two parallel pipelines spaced 0.5 m apart are...Ch. 4 - A small water droplet of diameter D=100m and...Ch. 4 - A tube of diameter 50 mm having a surface...Ch. 4 - Pressurized steam at 450K flows through a long,...Ch. 4 - The temperature distribution in laser-irradiated...Ch. 4 - Hot water at 85°C flows through a thin-walled...Ch. 4 - A furnace of cubical shape, with external...Ch. 4 - Laser beams are used to thermally process...Ch. 4 - A double-glazed window consists of two sheets of...Ch. 4 - A pipeline, used for the transport of crude oil,...Ch. 4 - A long power transmission cable is buried at a...Ch. 4 - A small device is used to measure the surface...Ch. 4 - A cubical glass melting furnace has exterior...Ch. 4 - An aluminum heat sink (k=240W/mK), used to cool an...Ch. 4 - Hot water is transported from a cogeneration power...Ch. 4 - A long constantan wire of 1-mm diameter is butt...Ch. 4 - A hole of diameter D=0.25m is drilled through the...Ch. 4 - In Chapter 3 we that, whenever fins are attached...Ch. 4 - An igloo is built in the shape of a hemisphere,...Ch. 4 - Prob. 4.34PCh. 4 - An electronic device, in the form of a disk 20 mm...Ch. 4 - The elemental unit of an air heater consists of a...Ch. 4 - Prob. 4.37PCh. 4 - Prob. 4.38PCh. 4 - Prob. 4.39PCh. 4 - Prob. 4.40PCh. 4 - One of the strengths of numerical methods is their...Ch. 4 - Determine expressionsfor...Ch. 4 - Consider heat transfer in a one-dimensional...Ch. 4 - In a two-dimensional cylindrical configuration,...Ch. 4 - Upper and lower surfaces of a bus bar are...Ch. 4 - Derive the nodal finite-difference equations for...Ch. 4 - Consider the nodal point 0 located on the boundary...Ch. 4 - Prob. 4.48PCh. 4 - Prob. 4.49PCh. 4 - Consider the network for a two-dimensional system...Ch. 4 - An ancient myth describes how a wooden ship was...Ch. 4 - Consider the square channel shown in the sketch...Ch. 4 - A long conducting rod of rectangular cross section...Ch. 4 - A flue passing hot exhaust gases has a square...Ch. 4 - Steady-state temperatures (K) at three nodal...Ch. 4 - Functionally graded materials are intentionally...Ch. 4 - Steady-state temperatures at selected nodal points...Ch. 4 - Consider an aluminum heat sink (k=240W/mK), such...Ch. 4 - Conduction within relatively complex geometries...Ch. 4 - Prob. 4.60PCh. 4 - The steady-state temperatures (°C) associated with...Ch. 4 - A steady-state, finite-difference analysis has...Ch. 4 - Prob. 4.63PCh. 4 - Prob. 4.64PCh. 4 - Consider a two-dimensional. straight triangular...Ch. 4 - A common arrangement for heating a large surface...Ch. 4 - A long, solid cylinder of diameter D=25mm is...Ch. 4 - Consider Problem 4.69. An engineer desires to...Ch. 4 - Prob. 4.71PCh. 4 - Prob. 4.72PCh. 4 - Prob. 4.73PCh. 4 - Refer to the two-dimensional rectangular plate of...Ch. 4 - The shape factor for conduction through the edge...Ch. 4 - Prob. 4.77PCh. 4 - A simplified representation for cooling in very...Ch. 4 - Prob. 4.84PCh. 4 - A long trapezoidal bar is subjected to uniform...Ch. 4 - Consider the system of Problem 4.54. The interior...Ch. 4 - A long furnace. constructed from refractory brick...Ch. 4 - A hot pipe is embedded eccentrically as shown in a...Ch. 4 - A hot liquid flows along a V-groove in a solid...Ch. 4 - Prob. 4S.5PCh. 4 - Hollow prismatic bars fabricated from plain carbon...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- It is decided to install several single-jet Pelton wheels to produce a total power of 18 MW. The available head is 246 m. The wheel rotational speed is 650 rpm and the speed ratio (❤) = 0.46. The diameter of the nozzle (jet) is limited to be 0.167 m with a Cv of 0.95. The efficiency of each turbine is 87%. Determine: (1) The number of Pelton wheels to be used, and (2) The bucket angle.arrow_forwardPlease show All work and fill it in thermodynamicsarrow_forwardQuick solution required. My request, Don't use Ai. Mechanical engineeringarrow_forward
- Please give handwritten solution, don't use chatgpt. Fbd should be includedarrow_forward(I) [40 Points] Using centered finite difference approximations as done in class, solve the equation for O: d20 dx² + 0.010+ Q=0 subject to the boundary conditions shown in the stencil below. Do this for two values of Q: (a) Q = 0.3, and (b) Q= √(0.5 + 2x)e-sinx (cos(5x)+x-0.5√1.006-x| + e −43*|1+.001+x* | * sin (1.5 − x) + (cosx+0.001 + ex-1250+ sin (1-0.9x)|) * x - 4.68x4. For Case (a) (that is, Q = 0.3), use the stencil in Fig. 1. For Case (b), calculate with both the stencils in Fig. 1 and Fig 2. For all the three cases, show a table as well as a plot of O versus x. Discuss your results. Use MATLAB and hand in the MATLAB codes. 1 0=0 x=0 2 3 4 0=1 x=1 Fig 1 1 2 3 4 5 6 7 8 9 10 11 0=0 x=0 0=1 x=1 Fig 2arrow_forwardFig 2 (II) [60 Points] Using centered finite difference approximation as done in class, solve the equation: 020 020 + მx2 მy2 +0.0150+Q=0 subject to the boundary conditions shown in the stencils below. Do this for two values of Q: (a) Q = 0.3, and (b) Q = 10.5x² + 1.26 * 1.5 x 0.002 0.008. For Case (a) (that is, Q = 0.3) use Fig 3. For Case (b), use both Fig. 3 and Fig 4. For all the three cases, show a table as well as the contour plots of versus (x, y), and the (x, y) heat flux values at all the nodes on the boundaries x = 1 and y = 1. Discuss your results. Use MATLAB and hand in the MATLAB codes. (Note that the domain is (x, y)e[0,1] x [0,1].) 0=0 0=0 4 8 12 16 10 Ꮎ0 15 25 9 14 19 24 3 11 15 0=0 8-0 0=0 3 8 13 18 23 2 6 сл 5 0=0 10 14 6 12 17 22 1 6 11 16 21 13 e=0 Fig 3 Fig 4 Textbook: Numerical Methods for Engineers, Steven C. Chapra and Raymond P. Canale, McGraw-Hill, Eighth Edition (2021).arrow_forward
- Ship construction question. Sketch and describe the forward arrangements of a ship. Include componets of the structure and a explanation of each part/ term. Ive attached a general fore end arrangement. Simplfy construction and give a brief describion of the terms.arrow_forwardProblem 1 Consider R has a functional relationship with variables in the form R = K xq xx using show that n ✓ - (OR 1.) = i=1 2 Их Ux2 Ихэ 2 (177)² = ² (1)² + b² (12)² + c² (1)² 2 UR R x2 x3arrow_forward4. Figure 3 shows a crank loaded by a force F = 1000 N and Mx = 40 Nm. a. Draw a free-body diagram of arm 2 showing the values of all forces, moments, and torques that act due to force F. Label the directions of the coordinate axes on this diagram. b. Draw a free-body diagram of arm 2 showing the values of all forces, moments, and torques that act due to moment Mr. Label the directions of the coordinate axes on this diagram. Draw a free body diagram of the wall plane showing all the forces, torques, and moments acting there. d. Locate a stress element on the top surface of the shaft at A and calculate all the stress components that act upon this element. e. Determine the principal stresses and maximum shear stresses at this point at A.arrow_forward
- 3. Given a heat treated 6061 aluminum, solid, elliptical column with 200 mm length, 200 N concentric load, and a safety factor of 1.2, design a suitable column if its boundary conditions are fixed-free and the ratio of major to minor axis is 2.5:1. (Use AISC recommended values and round the ellipse dimensions so that both axes are whole millimeters in the correct 2.5:1 ratio.)arrow_forward1. A simply supported shaft is shown in Figure 1 with w₁ = 25 N/cm and M = 20 N cm. Use singularity functions to determine the reactions at the supports. Assume El = 1000 kN cm². Wo M 0 10 20 30 40 50 60 70 80 90 100 110 cm Figure 1 - Problem 1arrow_forwardPlease AnswerSteam enters a nozzle at 400°C and 800 kPa with a velocity of 10 m/s and leaves at 375°C and 400 kPa while losing heat at a rate of 26.5 kW. For an inlet area of 800 cm2, determine the velocity and the volume flow rate of the steam at the nozzle exit. Use steam tables. The velocity of the steam at the nozzle exit is m/s. The volume flow rate of the steam at the nozzle exit is m3/s.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning

Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Understanding Conduction and the Heat Equation; Author: The Efficient Engineer;https://www.youtube.com/watch?v=6jQsLAqrZGQ;License: Standard youtube license