
Fundamentals of Heat and Mass Transfer
7th Edition
ISBN: 9780470917855
Author: Bergman, Theodore L./
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 4, Problem 4.10P
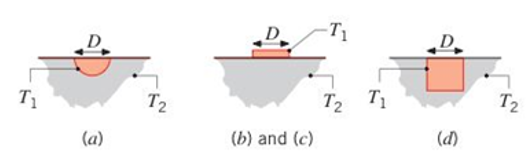
Based on the dimensionless conduction heat rates for cases 12—15 in Table 4.1b, find shape factors for the following objects having temperature
- A buried hemisphere, flush with the surface.
- A disk on the surface. Compare your result to Table 4.1a, case 10.
- A square on the surface.
- A buried cube, flush with the surface.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Show detailed step by step solution.
Topic: Thermodynamics
1. A simple cavity wall consists of two brick layers separated by an air gap of 50 mm. If the inside air temperature is 20oC and the ambient outside temperature is 5 oC, calculate the heat flux through the wall. Bricks are 100 mm thick with thermal conductivity kbrick = 0.5 W/m K, hin = 10 W/m2 K, hout = 20 W/m2 K. The internal air cavity can be considered still (no convection) with kair = 0.015 W/m K.
2. On a day in winter, the outside air temperature drops to -5 oC and the outside convective heat transfer changes to hout = (2 x V) + 8.9 W/m2 K. If the outside wind speed gusts at 50 kph, calculate the change in heat flux for the wall in question 3.
Two plane disks each 1.25 m in diameter are parallel and directly opposed to each other. They are separated by a distance of 0.5 m. Disk 1 is heated by electrical resistance to 833.3 K. Both disks are insulated on all faces except the two faces directly opposed to each other. Assume that the surroundings emit no radiation and that the disks are in space. Calculate the temperature of disk 2 at steady state and also the electrical energy input to disk 1. Hint: The fraction of heat lost from area 1 to space is (1 – F12).
The equation is shown below
Chapter 4 Solutions
Fundamentals of Heat and Mass Transfer
Ch. 4 - In the method of separation of variables (Section...Ch. 4 - A two-dimensional rectangular plate is subjected...Ch. 4 - Consider the two-dimensional rectangular plate of...Ch. 4 - A two-dimensional rectangular plate is subjected...Ch. 4 - A two-dimensional rectangular plate is subjected...Ch. 4 - Using the thermal resistance relations developed...Ch. 4 - Free convection heat transfer is sometimes...Ch. 4 - Consider Problem 4.5 for the case where the plate...Ch. 4 - Prob. 4.9PCh. 4 - Based on the dimensionless conduction heat rates...
Ch. 4 - Determine the heat transfer rate between two...Ch. 4 - A two-dimensional object is subjected to...Ch. 4 - An electrical heater 100 mm long and 5 mm in...Ch. 4 - Two parallel pipelines spaced 0.5 m apart are...Ch. 4 - A small water droplet of diameter D=100m and...Ch. 4 - A tube of diameter 50 mm having a surface...Ch. 4 - Pressurized steam at 450K flows through a long,...Ch. 4 - The temperature distribution in laser-irradiated...Ch. 4 - Hot water at 85°C flows through a thin-walled...Ch. 4 - A furnace of cubical shape, with external...Ch. 4 - Laser beams are used to thermally process...Ch. 4 - A double-glazed window consists of two sheets of...Ch. 4 - A pipeline, used for the transport of crude oil,...Ch. 4 - A long power transmission cable is buried at a...Ch. 4 - A small device is used to measure the surface...Ch. 4 - A cubical glass melting furnace has exterior...Ch. 4 - An aluminum heat sink (k=240W/mK), used to cool an...Ch. 4 - Hot water is transported from a cogeneration power...Ch. 4 - A long constantan wire of 1-mm diameter is butt...Ch. 4 - A hole of diameter D=0.25m is drilled through the...Ch. 4 - In Chapter 3 we that, whenever fins are attached...Ch. 4 - An igloo is built in the shape of a hemisphere,...Ch. 4 - Prob. 4.34PCh. 4 - An electronic device, in the form of a disk 20 mm...Ch. 4 - The elemental unit of an air heater consists of a...Ch. 4 - Prob. 4.37PCh. 4 - Prob. 4.38PCh. 4 - Prob. 4.39PCh. 4 - Prob. 4.40PCh. 4 - One of the strengths of numerical methods is their...Ch. 4 - Determine expressionsfor...Ch. 4 - Consider heat transfer in a one-dimensional...Ch. 4 - In a two-dimensional cylindrical configuration,...Ch. 4 - Upper and lower surfaces of a bus bar are...Ch. 4 - Derive the nodal finite-difference equations for...Ch. 4 - Consider the nodal point 0 located on the boundary...Ch. 4 - Prob. 4.48PCh. 4 - Prob. 4.49PCh. 4 - Consider the network for a two-dimensional system...Ch. 4 - An ancient myth describes how a wooden ship was...Ch. 4 - Consider the square channel shown in the sketch...Ch. 4 - A long conducting rod of rectangular cross section...Ch. 4 - A flue passing hot exhaust gases has a square...Ch. 4 - Steady-state temperatures (K) at three nodal...Ch. 4 - Functionally graded materials are intentionally...Ch. 4 - Steady-state temperatures at selected nodal points...Ch. 4 - Consider an aluminum heat sink (k=240W/mK), such...Ch. 4 - Conduction within relatively complex geometries...Ch. 4 - Prob. 4.60PCh. 4 - The steady-state temperatures (°C) associated with...Ch. 4 - A steady-state, finite-difference analysis has...Ch. 4 - Prob. 4.63PCh. 4 - Prob. 4.64PCh. 4 - Consider a two-dimensional. straight triangular...Ch. 4 - A common arrangement for heating a large surface...Ch. 4 - A long, solid cylinder of diameter D=25mm is...Ch. 4 - Consider Problem 4.69. An engineer desires to...Ch. 4 - Prob. 4.71PCh. 4 - Prob. 4.72PCh. 4 - Prob. 4.73PCh. 4 - Refer to the two-dimensional rectangular plate of...Ch. 4 - The shape factor for conduction through the edge...Ch. 4 - Prob. 4.77PCh. 4 - A simplified representation for cooling in very...Ch. 4 - Prob. 4.84PCh. 4 - A long trapezoidal bar is subjected to uniform...Ch. 4 - Consider the system of Problem 4.54. The interior...Ch. 4 - A long furnace. constructed from refractory brick...Ch. 4 - A hot pipe is embedded eccentrically as shown in a...Ch. 4 - A hot liquid flows along a V-groove in a solid...Ch. 4 - Prob. 4S.5PCh. 4 - Hollow prismatic bars fabricated from plain carbon...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- 2.3 The shield of a nuclear reactor is idealized by a large 25-cm-thick flat plate having a thermal conductivity of . Radiation from the interior of the reactor penetrates the shield and there produces heat generation that decreases exponentially from a value of at the inner surface to a value of at a distance of 12.5 cm from the interior surface. If the exterior surface is kept at 38°C by forced convection, determine the temperature at the inner surface of the field. Hint: First set up the differential equation for a system in which the heat generation rate varies according to .arrow_forward1- The energy transferred from the anterior chamber of the eye through the cornea varies considerably depending on whether a contact lens is worn. Treat the eye as a spherical system and assume the system to be at steady state. The convection coefficient ho is unchanged with and without the contact lens in place. The cornea and the lens cover one-third of the spherical surface area. T he T h Anterior chamber Contact lens Cornea are as follows: Values of the parameters representing this situation r 10.2mm, r 12.7 mm, r3= 16.5 mm, Teoj= 37°C, Teoo = 21°C, ki = 0.35 W/m.K, k2 0.80 W/m.K, h 12 W/m2.K, ho 12 W/m2.K. (a) Construct the thermal circuits, labeling all potential and flows form the systems excluding the contact lens and including the contact lens. Write resistance elements in terms of appropriate parameters (b) Determine the heat loss from the interior chamber with and without the contact lens in place (c) Discuss the implication of your results.arrow_forwardFig. 4 illustrates an insulating wall of three homogeneous layers with conductivities k1, k2, and k3 in intimate contact. Under steady state conditions, both right and left surfaces are exposed to a temperature in a steady state condition at ambient temperatures of T and T , respectively, while ß, and BLare the film coefficients respectively. Assume that there is no internal heat generation and that the heat flow is one-dimensional (dT/dy = 0). For the illustrated ambient temperature in Fig. 4, determine the temperature's distribution at each layer. Material 3 Material 1 Material 2 T= 100 T= 35 °C Kı=20 K3=50 (W/m.k) K3=30 (W/m.k) B1= 10 w/m² °K (W/m.k) BR= 15 w/m²°K 50 mm 35 mm 25 cm Fig. 4arrow_forward
- i. Calculate the heat loss through the furnace wall (all sides) by using conduction shape factor. ii. Calculate the heat loss through the furnace wall by using thermal resistance from each side (6 sides). iii. Determine the percentage difference of heat loss between case (i) and case (ii). iv. Explain why the heat transfer for both cases are different.arrow_forwardOne side of a copper slab receives a net heat input at a rate of 5000 W due to radiation. The other face is held at a temperature of 35 °C. If steady-state conditions prevail, calculate the surface temperature of the side receiving radiant energy. The surface area of each face is 0.05 m², and the slab thickness is 4 cm. (For copper: k = 398 W/(m.K)) (To = 45.1 °C)arrow_forward2. A heater is a thin vertical panel 1.0m long and 0.7m high and is used in a warehouse to keep workers warm. The heater has air circulating on each side. Assume the maximum temperature of the panel is 60°C (already above the board line that is safe for human hands to touch briefly without getting hurt). Assume the room air temperature is 18°C but the warehouse wall temperature is 5°C. Model the surface with an emittance of 0.9 and Vair = 1.57x105 m²/s. a. Determine the maximum power rating for the heater. b. Now if you run the heat by standing on its side (it will be 1.0 m high and 0.7 m long), determine the surface temperature. c. Compare case a and b and explain any differences you see.arrow_forward
- PROBLEM 1: The block of 304 stainless steel shown below is well insulated on the front and back surfaces, and the temperature in the block varies linearly in both the x- and y-directions. Find: (a) The heat fluxes and heat flows in the x- and y-directions. (b) The magnitude and direction of the heat flux vector. 15°C 5°C 5 cm y 5 cm- 10 cm The thermal conductivity of 304 stainless steel is 14.4 W/m K. 10°C 0°Carrow_forwardA warehouse is being built that will have neither heating nor cooling. Depending on the amount of insulation, the time constant for the building may range from 1 to 4 hr. To illustrate the effect insulation will have on the temperature inside the warehouse, assume the outside temperature varies as a sine wave, with a minimum of 12°C at 2:00 A.M. and a maximum of 32°C at 2:00 P.M. Assuming the exponential term (which involves the initial temperature To) has died off, what is the lowest temperature inside the building if the time constant is 1 hr? If it is 4 hr? What is the highest temperature inside the building if the time constant is 1 hr? If it is 4 hr? If the time constant is 1 hr, then the lowest temperature inside the building is about °C. (Round to the nearest tenth as needed.)arrow_forwardHi, kindly solve this problem and show the solution. Thank youarrow_forward
- Consider the square channel shown in the sketch operating under steady state condition. The inner surface of the channel is at a uniform temperature of 600 K and the outer surface is at a uniform temperature of 300 K. From a symmetrical elemental of the channel, a two-dimensional grid has been constructed as in the right figure below. The points are spaced by equal distance. Tout = 300 K k = 1 W/m-K T = 600 K (a) The heat transfer from inside to outside is only by conduction across the channel wall. Beginning with properly defined control volumes, derive the finite difference equations for locations 123. You can also use (n, m) to represent row and column. For example, location Dis (3, 3), location is (3,1), and location 3 is (3,5). (hint: I have already put a control volume around this locations with dashed boarder.) (b) Please use excel to construct the tables of temperatures and finite difference. Solve for the temperatures of each locations. Print out the tables in the spread…arrow_forwardMicrowave ovens operate by rapidly aligning and reversing water molecules within the food, resulting in volumetric energy generation and, in turn, cooking of the food. When the food is initially frozen, however, the water molecules do not readily oscillate in response to the microwaves, and the volumetric generation rates are between one and two orders of magnitude lower than if the water were in liquid form. (Microwave power that is not absorbed in the food is reflected back to the microwave generator, where it must be dissipated in the form of heat to prevent damage to the generator.) (a) Consider a frozen, 0.7-kg spherical piece of ground beef at an initial temperature of T₁ = -20°C placed in a microwave oven with To = 30°C and h = 15 W/m².K. Determine how long, in min, it will take the beef to reach a uniform temperature of T = 0°C, with all the water in the form of ice. Assume the properties of the beef are the same as ice, and assume 3% of the oven power (P = 1 kW total) is…arrow_forwardDon’t use Heissler charts to answer this question Heat sterilization of lumber, timbers, and pallets is used to kill insects to prevent their transfer between countries in international trade. This is analogous to food sterilization by heat. A typical requirement here is that the slowest heating point of any woodconfiguration be held at 56 °C for 30 minutes. Consider hot air heating of wooden boards that maintains their surface temperature at 70 °C. The boards are stacked outside and in the winter time they can be considered to be at 0 °Cwhen theyare brought in for heating. The thermal diffusivity of the wood is 9*10-8m2/s. a.Calculate the time from the start of heating for a 2.5 cm thick board to reach a sterilization temperature of 56 °C at its slowest heating point .b.Calculate the heating time when four such boards are stacked together. c.Calculate the ratio of the two heating times (for a single board versus when they are stacked), and explain the ratio. Note: You’re free to…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning

Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Understanding Conduction and the Heat Equation; Author: The Efficient Engineer;https://www.youtube.com/watch?v=6jQsLAqrZGQ;License: Standard youtube license