Chapter 4, Problem 4.59P

Conduction within relatively complex geometries can sometimes be evaluated using the finite-difference methods of this text that are applied to subdomains and patched together. Consider the two-dimensional domain formed by rectangular and cylindrical subdomains patched at the common, dashed control surface. Note that, along the dashed control surface, temperatures in the two subdomains are identical and local conduction heat fluxes to the cylindrical subdomain are identical to local conduction heat fluxes from the rectangular subdomain.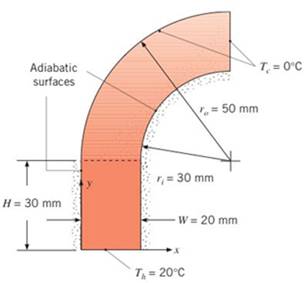

Calculate the heat transfer per unit depth into the page, $q\text{'},$ using $\Delta x=\Delta y=\Delta r=10\text{mm}$ and $\Delta \varphi =\pi /8.$ The base of the rectangular subdomain is held at $T_h=20°\text{C,}$ while the vertical surface of the cylindrical subdomain and the surface at outer radius $r_o$ are at $T_c=0°\text{C}\text{.}$ remaining surfaces are adiabatic. and the thermal conductivity is $k=10\text{W/m}\cdot \text{K}\text{.}$