Chapter 3.3, Problem 73AYU

Analyzing the Motion of a Projectile A projectile is fired from a cliff $200$ feet above the water at an inclination of $45°$ to the horizontal, with a muzzle velocity of $50$ feet per second. The height $h$ of the projectile above the water is modeled by

$h(x)=\frac{-32x^2}{{50}^2}+x+200$

Where $x$ is the horizontal distance of the projectile from the face of the cliff.

At what horizontal distance from the face of the cliff is the height of the projectile a maximum?

Find the maximum height of the projectile.

At what horizontal distance from the face of the cliff will the projectile strike the water?

Graph the function $h$, $0\le x\le 200$.

Use a graphing utility to verify the solutions found in parts $(b)$ and $(c)$.

When the height of the projectile is $100$ feet above the water, how far is it from the cliff ?

To determine

To calculate: The horizontal distance from face of the cliff at which the height of the projectile is a maximum.

Answer to Problem 73AYU

Solution:

The height of projectile is maximum at a distance of $39.0625feet$ from the face of the cliff.

Explanation of Solution

Given Information:

A projectile is fired from a cliff 200 feet above the water at an inclination of ${45}^{\circ }$ to the horizontal, with a muzzle velocity of 50 feet per second. The height $h$ of the projectile above the water is modelled by $h(x)=\frac{-32x^2}{{50}^2}+x+200$, where $x$ is the horizontal distance of projectile from the face of the cliff.

Formula used:

The graph of the function $f(x)=a{x}^2+bx+c$ is a parabola and it has the maximum height at vertex given as $\left(\frac{-b}{2a},f\left(\frac{-b}{2a}\right)\right)$

Calculation:

A projectile is fired from a cliff 200 feet above the water at an inclination of ${45}^{\circ }$ to the horizontal with a muzzle velocity of 50 feet per second. The height $h$ of the projectile above the water is modelled by $h(x)=\frac{-32x^2}{{50}^2}+x+200$, where $x$ is the horizontal distance of projectile from the face of the cliff.

The graph of the function $f(x)=a{x}^2+bx+c$ is a parabola and it has the maximum height at vertex given as $\left(\frac{-b}{2a},f\left(\frac{-b}{2a}\right)\right)$

Compare $h(x)=\frac{-32x^2}{{50}^2}+x+200$ with $f(x)=a{x}^2+bx+c$

$a=\frac{-32}{{50}^2},b=1,c=200$

$\frac{-b}{2a}=\frac{-1}{2\left(\frac{-32}{{50}^2}\right)}=\frac{{50}^2}{64}=39.0625$

Hence, the height of projectile is maximum at a distance $39.0625feet$ from the face of the cliff.

To determine

To calculate: The maximum height of the projectile.

Answer to Problem 73AYU

Solution:

The maximum height of the projectile is $219.53125feet$.

Explanation of Solution

Given Information:

A projectile is fired from a cliff 200 feet above the water at an inclination of ${45}^{\circ }$ to the horizontal with a muzzle velocity of 50 feet per second. The height $h$ of the projectile above the water is modelled by $h(x)=\frac{-32x^2}{{50}^2}+x+200$, where $x$ is the horizontal distance of projectile from the face of the cliff.

Formula used:

The graph of the function $f(x)=a{x}^2+bx+c$ is a parabola and it has the maximum height at vertex given as $\left(\frac{-b}{2a},f\left(\frac{-b}{2a}\right)\right)$

Calculation:

A projectile is fired from a cliff 200 feet above the water at an inclination of ${45}^{\circ }$ to the horizontal with a muzzle velocity of 50 feet per second. The height $h$ of the projectile above the water is modelled by $h(x)=\frac{-32x^2}{{50}^2}+x+200$, where $x$ is the horizontal distance of projectile from the face of the cliff.

The graph of the function $f(x)=a{x}^2+bx+c$ is a parabola and it has the maximum height at vertex given as $\left(\frac{-b}{2a},f\left(\frac{-b}{2a}\right)\right)$

Compare $h(x)=\frac{-32x^2}{{50}^2}+x+200$ with $f(x)=a{x}^2+bx+c$

$a=\frac{-32}{{50}^2},b=1,c=200$

$\frac{-b}{2a}=\frac{-1}{2\left(\frac{-32}{{50}^2}\right)}=\frac{{50}^2}{64}=39.0625$

$f\left(\frac{-b}{2a}\right)=f(39.0625)$

$\Rightarrow f(39.0625)=\frac{-32}{{50}^2}{\left(39.0625\right)}^2+(39.0625)+200$

$\Rightarrow f(39.0625)=219.53125$

The maximum height of projectile is $219.53125feet$.

To determine

To calculate: The horizontal distance from the face of the cliff at which the projectile will strike the water.

Answer to Problem 73AYU

Solution:

The projectile will strike the water at $170.024feet$ from the face of the cliff.

Explanation of Solution

Given Information:

A projectile is fired from a cliff 200 feet above the water at an inclination of ${45}^{\circ }$ to the horizontal, with a muzzle velocity of 50 feet per second. The height $h$ of the projectile above the water is modelled by $h(x)=\frac{-32x^2}{{50}^2}+x+200$, where $x$ is the horizontal distance of projectile from the face of the cliff.

Formula used:

When the projectile touches the water the height of the projectile becomes zero.

$\Rightarrow h(x)=0$

Calculation:

A projectile is fired from a cliff 200 feet above the water at an inclination of ${45}^{\circ }$ to the horizontal, with a muzzle velocity of 50 feet per second. The height $h$ of the projectile above the water is modelled by $h(x)=\frac{-32x^2}{{50}^2}+x+200$, where $x$ is the horizontal distance of projectile from the face of the cliff.

When the projectile touches the water the height of the projectile becomes zero.

$\Rightarrow h(x)=0$

$\Rightarrow \frac{-32x^2}{{50}^2}+x+200=0$

The least common denominator is ${50}^2$

$\Rightarrow \frac{-32x^2+{50}^{2}x+{(50)}^{2}200}{{50}^2}=0$

$\Rightarrow -32x^2+2500x+500000=0$

Divide by $-4$ on both sides

$8x^2-625x-125000=0$

The equation $8x^2-625x-125000=0$ is solved by using quadratic formula as

$x=\frac{-(-625)\pm \sqrt{{(-625)}^2-4(8)(-125000)}}{2(8)}$

$=\frac{625\pm \sqrt{390625+4000000}}{16}$

$=\frac{625\pm \sqrt{4390625}}{16}$

$x=\frac{625\pm 2095.4}{16}$

$=\frac{625+2095.4}{16}$ or $=\frac{625-2095.4}{16}$

$=170.024$ or $=-91.9$

As $x$ is the horizontal distance of projectile from the face of the cliff, so $x$ is always positive.

$\Rightarrow x=170.024$

The projectile will strike the water at $170.025feet$ from the face of the cliff.

To determine

To graph: To graph $h(x)=\frac{-32x^2}{{50}^2}+x+200,0\le x\le 200$

Explanation of Solution

Given Information:

$h(x)=\frac{-32x^2}{{50}^2}+x+200,0\le x\le 200$

Graph:

The equation of $h$ is $h(x)=\frac{-32x^2}{{50}^2}+x+200,0\le x\le 200$

To graph $h$ using graphing utility, follow the steps given below

Step 1: Press Y= and enter the expression $x^2+\frac{40}{x}$ in the numerator and enter $(0\le x)and(x\le 200)$ in the denominator.

Press [2^nd][MATH] to write the inequality

Press [2^nd][MATH][$⊳$] to get “and”

Step 2: Press [GRAPH].

The graph will be as given below

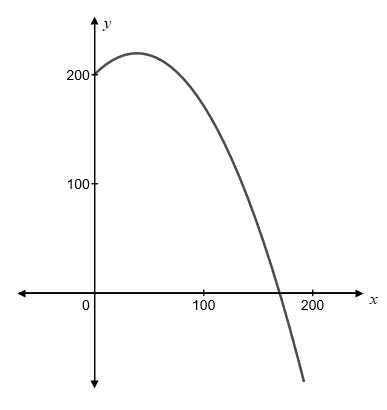
Interpretation:

The graph of the equation $h(x)=\frac{-32x^2}{{50}^2}+x+200,0\le x\le 200$ shows more than half part of the parabola.

To determine

To calculate: The maximum and zeros of $h(x)=\frac{-32x^2}{{50}^2}+x+200$.

Answer to Problem 73AYU

Solution:

Maximum of $h(x)=\frac{-32x^2}{{50}^2}+x+200$ is $219.53125$ and zero of the function $h(x)=\frac{-32x^2}{{50}^2}+x+200$ is at $170.024$.

Explanation of Solution

Given Information:

$h(x)=\frac{-32x^2}{{50}^2}+x+200$

Calculation:

The equation of $h$ is $h(x)=\frac{-32x^2}{{50}^2}+x+200$

To find the zero and maximum of $h$ using graphing utility follow the steps given below

Step 1: Press Y= and enter the expression $\frac{-32x^2}{{50}^2}+x+200$

Step 2: Press [2^nd][TRACE] to get the CALC. Under CALC menu choose 2: zero and press

ENTER.

Step 3: Move the cursor( use arrow keys ) to left of observed zero location. Press ENTER.

Step 4: Move the cursor( use arrow keys ) to right of observed zero location. Press ENTER.

Step 5: When last screen asks for guess press ENTER.

The coordinates of zeros are $\left(-91.90,0\right),(170.024,0)$

As the distance and height can’t be negative, the co-ordinate of zero is $(170.024,0)$

Step 6: Press [2ND][TRACE] to get the CALC. Under CALC menu choose 3: maximum and press ENTER.

Step 7: Move the cursor (use arrow keys) to left of observed maximum location. Press ENTER.

Step 8: Move the cursor( use arrow keys ) to right of observed maximum location. Press ENTER.

Step 9: When last screen asks for guess, press ENTER

The coordinate of maximum value is $(39.0625,219.53125)$.

From part (b) the maximum height is $219.53125$ and from part (c) the zero of the height function is $170.024$

Hence, using graphical utility the maximum height and the zero of the function coincides with the answers from part (b) and part (c).

To determine

To calculate: The distance of the projectile from the cliff, when it is 100 feet above the water.

Answer to Problem 73AYU

Solution:

The distance of projectile from the cliff is $135.7feet$, when it is 100 feet above the water.

Explanation of Solution

Given Information:

A projectile is fired from a cliff 200 feet above the water at an inclination of ${45}^{\circ }$ to the horizontal with a muzzle velocity of 50 feet per second. The height $h$ of the projectile above the water is modelled by $h(x)=\frac{-32x^2}{{50}^2}+x+200$, where $x$ is the horizontal distance of projectile from the face of the cliff.

Formula used:

$h(x)=\frac{-32x^2}{{50}^2}+x+200$

Calculation:

A projectile is fired from a cliff 200 feet above the water at an inclination of ${45}^{\circ }$ to the horizontal with a muzzle velocity of 50 feet per second. The height $h$ of the projectile above the water is modelled by $h(x)=\frac{-32x^2}{{50}^2}+x+200$

Where $x$ is the horizontal distance of projectile from the face of the cliff

The projectile is 100 feet above the water.

$\Rightarrow h(x)=100$

$\frac{-32x^2}{{50}^2}+x+200=100$

The least common denominator is ${50}^2$

$\frac{-32x^2+{50}^{2}x+{(50)}^{2}200}{{50}^2}=\frac{100{(50)}^2}{{50}^2}$

$-32x^2+2500x+500000=250000$

Divide by $-4$ on both sides

$8x^2-625x-125000=-62500$

Add $62500$ on both sides

$8x^2-625x-62500=0$

The equation $8x^2-625x-62500=0$ is solved by using quadratic formula as

$x=\frac{-(-625)\pm \sqrt{{(-625)}^2-4(8)(-62500)}}{2(8)}$

$x=\frac{625\pm \sqrt{390625+2000000}}{16}$

$x=\frac{625\pm \sqrt{2390625}}{16}$

$x=\frac{625\pm 1546.2}{16}$

$x=\frac{625+1546.2}{16}$ or $x=\frac{625-1546.2}{16}$

$x=135.7$ or $x=-57.575$

As $x$ is the horizontal distance of projectile from the face of the cliff, so $x$ is always positive.

$\Rightarrow x=135.7$

The distance of projectile from the cliff is $135.7feet$, when it is 100 feet above the water.