
In Problems 49-54, determine the quadratic function whose graph is given.
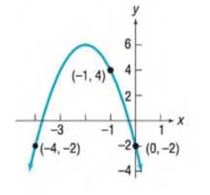
To calculate: The quadratic function using the given graphs.
Answer to Problem 52AYU
The equation of the given graph is .
Explanation of Solution
Given:
The given graph is
Formula Used:
The general form of a quadratic equation is
This general equation can also be written as , where
If , the graph opens upwards.
If , the graph opens downwards.
The vertex of the above function is .
The axis of symmetry will be .
We can find the by equating the equation at .
We can find the by equation the equation at .
1. If then the vertex is the .
2. If then the graph has no .
3. If then the vertex is the .
Calculation:
Let us consider the quadratic equation of the given graph to be
-----(1)
From the given graph, we can see that the of the given function is .
We know that the is the value of the function at , thus, we have
-----(2)
At , (1) becomes
-----(3)
Thus, using (2) and (3), we get the value of .
Thus, equation (1) becomes
-----(4)
Now, we need to find and .
We know that a point in a graph is written as .
The given graph has 2 points and .
Consider the point .
Here, we have and .
Therefore, substituting it in (4), we get
-----(5)
Now, consider the point .
Here, we have and .
Therefore, substituting it in (4), we get
-----(6)
In order to find the values of and , we have to solve the equations (5) and (6).
Therefore, we have
-----(5) And
-----(6).
Now, on subtracting (5) and (6), we get
On substituting the above value in (5), we get
Therefore, the equation of the given graph is
Chapter 3 Solutions
Precalculus
Additional Math Textbook Solutions
University Calculus: Early Transcendentals (4th Edition)
Calculus: Early Transcendentals (2nd Edition)
Algebra and Trigonometry (6th Edition)
Elementary Statistics (13th Edition)
Thinking Mathematically (6th Edition)
Pre-Algebra Student Edition
- Explain the relationship between 12.3.6, (case A of 12.3.6) and 12.3.7arrow_forwardExplain the key points and reasons for the establishment of 12.3.2(integral Test)arrow_forwardUse 12.4.2 to determine whether the infinite series on the right side of equation 12.6.5, 12.6.6 and 12.6.7 converges for every real number x.arrow_forward
- use Corollary 12.6.2 and 12.6.3 to derive 12.6.4,12.6.5, 12.6.6 and 12.6.7arrow_forwardExplain the focus and reasons for establishment of 12.5.1(lim(n->infinite) and sigma of k=0 to n)arrow_forwardExplain the focus and reasons for establishment of 12.5.3 about alternating series. and explain the reason why (sigma k=1 to infinite)(-1)k+1/k = 1/1 - 1/2 + 1/3 - 1/4 + .... converges.arrow_forward
- Explain the key points and reasons for the establishment of 12.3.2(integral Test)arrow_forwardUse identity (1+x+x2+...+xn)*(1-x)=1-xn+1 to derive the result of 12.2.2. Please notice that identity doesn't work when x=1.arrow_forwardExplain the key points and reasons for the establishment of 11.3.2(integral Test)arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





