Chapter 3.3, Problem 27AYU

In Problems 21-32, graph the function $f$ by starting with the graph of $y=x^2$ and using transformations (shifting, compressing, stretching, and/or reflection). Verify your results using a graphing utility.

[ Hint: If necessary, write $f$ in the form $f\left(x\right)=a{(x-h)}^2+k$.]

$f(x)=-x^2-2x$

To determine

To graph: The transformation of the function $f(x)=-x^2-2x$.

Answer to Problem 27AYU

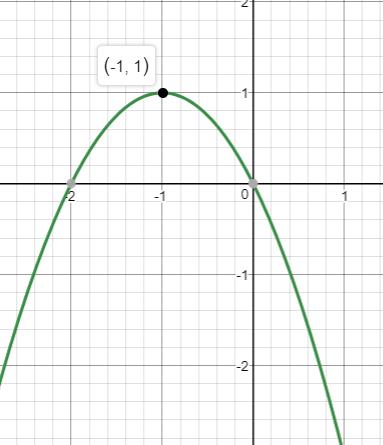
Explanation of Solution

Given:

We have to graph the function $f(x)=-x^2-2x$.

Graph:

The graph of the given function is

Interpretation:

The graph of $f(x)=a{x}^2,a=1$ is

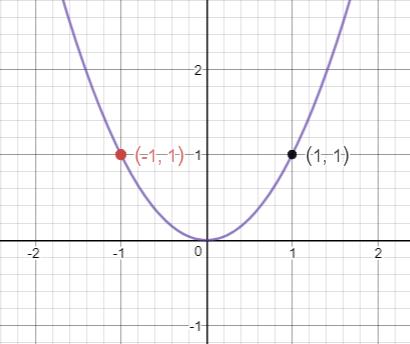
Now, we can graph the given function by transforming the above graph.

The given function is $f(x)=-x^2-2x$.

The general form of a quadratic function is $g(x)=a{\left(x-h\right)}^2+k$.

Here, if $a<0$, the graph opens upward otherwise the graph opens downwards.

If $a$ is closer to 0, then the graph is shorter and wider.

If $a$ is large, then the graph is tall and narrow.

Then, the graph of $g(x)$ is the graph of $f(x)$ with $h$ units shifted horizontally and $k$ units shifted vertically.

Here, we can convert the given equation into the standard form by using the square completion technique.

The given equation can also be written as $f(x)=-(x^2+2x)$

Therefore, let us now add and subtract the square of half of the $x\text{-coefficient}$ in the given equation.

Therefore, we get

$\begin{array}{l}f(x)=-(x^2+2x)\\ \Rightarrow -\left(x^2+2x+{\left(\frac{2}{2}\right)}^2-{\left(\frac{2}{2}\right)}^2\right)\\ \Rightarrow -\left(x^2+2x+{\left(1\right)}^2-{\left(1\right)}^2\right)\\ \Rightarrow -\left({\left(x+1\right)}^2-1\right)\\ \Rightarrow -\left({\left(x+1\right)}^2\right)+1\end{array}$

Thus, the given equation can be written in the standard form as $f(x)=-{\left(x+1\right)}^2+1$.

Since, $a=-1$ is positive, the graph opens downwards.

In the given function, we have $h=-1$ and $k=1$, therefore, the graph is the graph of $f(x)=x^2$ opening downwards with 1 units shifted horizontally left and 1 units shifted vertically upwards.