
Concept explainers
(a)
To find: The slope and y-intercept of linear function
(a)
Answer to Problem 4RE
Slope
y-intercept
Explanation of Solution
Given:
Slope: The coefficient of x of linear function.
Slope
y-intercept: The constant part of the function.
y-intercept
(b)
To find:Theaverage rate of change of function
(b)
Answer to Problem 4RE
Explanation of Solution
Given:
The average rate of change of linear function is constant. Average rate is change in y over change in x.
In another way, It would be slope of linear function.
Therefore, the average rate is
(c)
To graph: Thelinear function
(c)
Answer to Problem 4RE
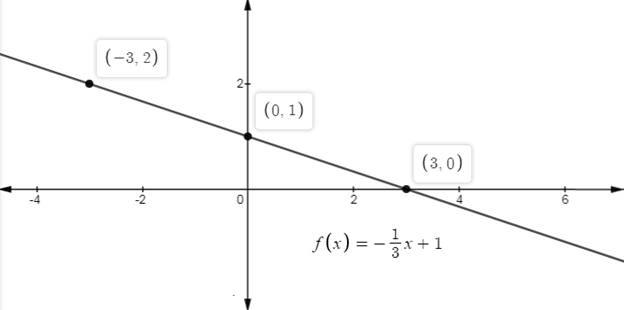
Explanation of Solution
Given:
The given linear function,
First make the table of x and y. By taking some random value of x
Now plot the points on graph.
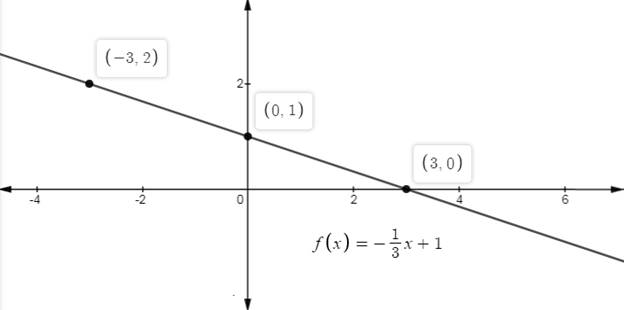
(d)
To find: The increasing, decreasing or constant of function
(d)
Answer to Problem 4RE
decreasing
Explanation of Solution
Given:
The average rate of change of linear function is constant. Average rate is change in y over change in x.
In another way, It would be slope of linear function.
The rate of the function is negative. If the rate of linear function is negative then it would be decreasing function.
Chapter 3 Solutions
Precalculus
Additional Math Textbook Solutions
Pre-Algebra Student Edition
College Algebra with Modeling & Visualization (5th Edition)
Introductory Statistics
Thinking Mathematically (6th Edition)
Calculus: Early Transcendentals (2nd Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
- Let the region R be the area enclosed by the function f(x)= = 3x² and g(x) = 4x. If the region R is the base of a solid such that each cross section perpendicular to the x-axis is an isosceles right triangle with a leg in the region R, find the volume of the solid. You may use a calculator and round to the nearest thousandth. y 11 10 9 00 8 7 9 5 4 3 2 1 -1 -1 x 1 2arrow_forwardLet the region R be the area enclosed by the function f(x) = ex — 1, the horizontal line y = -4 and the vertical lines x = 0 and x = 3. Find the volume of the solid generated when the region R is revolved about the line y = -4. You may use a calculator and round to the nearest thousandth. 20 15 10 5 y I I I | I + -1.5 -1 -0.5 0.5 1 1.5 2 2.5 3 -5 I -10 -15 I + I I T I I + -20 I + -25 I I I -30 I 3.5 4 xarrow_forwardplease show all the workarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





