Chapter 3.1, Problem 52AYU

(a)

To determine

To plot:the ordered pairs in a Cartesian plane.

Answer to Problem 52AYU

The Cartesian plane is:

  

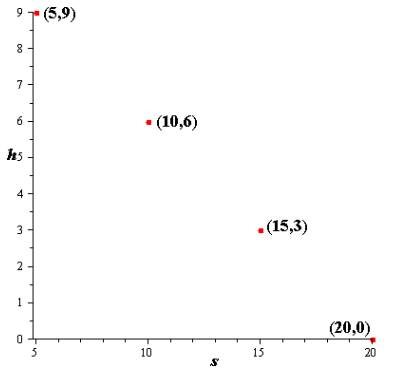
Explanation of Solution

Given:

Soda, $s$	Hot Dogs, $h$
$20$	$0$
$15$	$3$
$10$	$6$
$5$	$9$

Explanations:

Let us consider the following table

Soda, <$s$	Hot Dogs, $h$
$20$	$0$
$15$	$3$
$10$	$6$
$5$	$9$

The ordered pairs $\left(p,q\right)$ in Cartesian plain is as follows

  

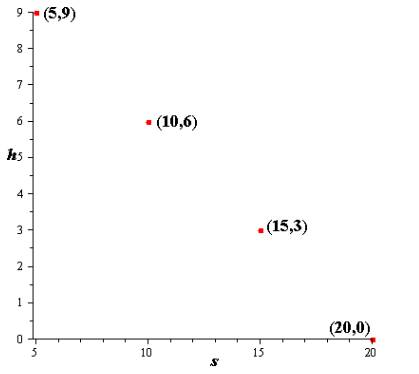
Conclusion:

Therefore, theordered pairs are plotted.

(b)

To determine

To show:number of hot dogs purchased is a linear function of the number of sodas purchased

Answer to Problem 52AYU

Hence, number of hot dogs purchased is a linear function of the number of sodas purchased $s$ .

Explanation of Solution

Proof:

If average rate of change is constant then function is linear.

Hence, find average rate of change of the function at different points as

point	Average rate of change,   $\frac{\Delta h}{\Delta s}$
$(20,0)$ and   $(15,3)$	$\frac{3-0}{15-20}=-\frac{3}{5}$
$(15,3)$ and   $(10,6)$	$\frac{6-3}{10-15}=-\frac{3}{5}$
$(10,6)$ and   $(5,9)$	$\frac{9-6}{5-10}=-\frac{3}{5}$

It is clear that the average rate of function is constant; hence number of hot dogs purchased is a linear function of the number of sodas purchased $s$ .

Conclusion:

Hence, number of hot dogs purchased is a linear function of the number of sodas purchased.

(c)

To determine

the linear function which describes the relation between $s$ and $h$ .

Answer to Problem 52AYU

Hence, the linear function that describes the relation between $s$ and $h$ is $h=-0.6s+12$

Explanation of Solution

Calculation:

To determine the linear function describing the relation between $s$ and $h$ , let us consider any two points, say $\left(20,0\right)$ and $\left(10,6\right)$

The equation of the line passing through two points $\left(x_1,y_1\right)$ and $\left(x_2,y_2\right)$ is $\left(y-y_1\right)=\left(\frac{y_2-y_1}{x_2-x_1}\right)\left(x-x_1\right)$

Similarly, equation of line passing through $\left(20,0\right)$ and $\left(10,6\right)$ is

  $\begin{array}{l}\left(y-0\right)=\frac{6-0}{10-20}\left(x-20\right)\\ y=\frac{6}{-10}\left(x-20\right)\\ y=-\frac{3}{5}x+12\end{array}$

Where $y=h$ and $x=s$ , therefore

  $h=-\frac{3}{5}s+12$

Hence, the linear function that describes the relation between $s$ and $h$ is $h=-0.6s+12$

Conclusion:

Hence, the linear function that describes the relation between $s$ and $h$ is $h=-0.6s+12$

(d)

To determine

To find: the implied domain of the linear function

Answer to Problem 52AYU

Hence, the implied domain of the linear function is $\left[0,20\right]$

Explanation of Solution

Explanations:

The graph of the linear function cannot be negative; therefore, the graph will terminate there where it becomes zero.

  $\begin{array}{l}h=0\\ -0.6s+12=0\\ 0.6s=12\\ s=20\end{array}$

Hence, the implied domain of the linear function is $\left[0,20\right]$

Conclusion:

Hence, the implied domain of the linear function is $\left[0,20\right]$

(e)

To determine

To graph: the linear function found in part (a).

Answer to Problem 52AYU

The graph of the linear function is:

  

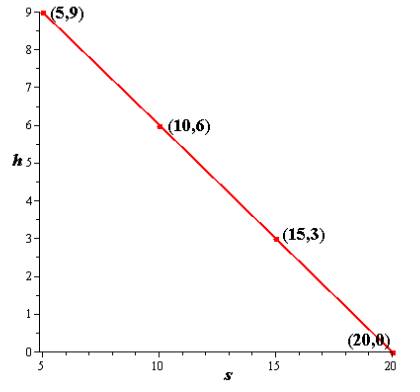
Explanation of Solution

Calculation:

The graph of the linear function in the Cartesian plane drawn in part (a) is as follows

  

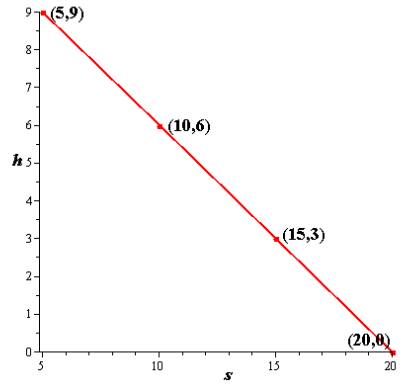
Conclusion:

The graph of the linear function is drawn.

(f)

To determine

To interpret:the slope.

Answer to Problem 52AYU

Hence, slope of the function $h=-0.6s+12$ is $-0.6$ .

Explanation of Solution

Calculation:

  $h=-0.6s+12$

The linear function is to the form $f\left(x\right)=mx+b$ , where $m$ is the slope of the graph of the function which is straight line and $b$ is the $y-\mathrm{int}ercept$ .

Hence, slope of the function $h=-0.6s+12$ is $-0.6$ .

Conclusion:

Hence, slope of the function $h=-0.6s+12$ is $-0.6$ .

(g)

To determine

To interpret:the values of the intercepts.

Answer to Problem 52AYU

  $\text{s-intercept}$ is $20$ and $\text{h-intercept}$ is $12$

Explanation of Solution

Calculation:

The $\text{h-intercept}$ is $12$ and $\text{s-intercept}$ can be found by putting $h=0$ in the function as

  $\begin{array}{l}h=-0.6s+12\\ 0.6s+12=0\\ 0.6s=12\\ s=20\end{array}$

Hence, $\text{s-intercept}$ is $20$

Conclusion:

Hence, $\text{s-intercept}$ is $20$ and $\text{h-intercept}$ is $12$