Chapter 3.4, Problem 11AYU

Analyzing the Motion of a Projectile A projectile is fired from a cliff 200 feet above the water at an inclination of ${45}^{\circ }$ to the horizontal, with a muzzle velocity of 50 feet per second. The height $h$ of the projectile above the water is modeled by

$h\left(x\right)=\frac{-32x^2}{{\left(50\right)}^2}+x+200$

where $x$ is the horizontal distance of the projectile from the face of the cliff.

(a) At what horizontal distance from the face of the cliff is the height of the projectile a maximum?

(b) Find the maximum height of the projectile.

(c) At what horizontal distance from the face of the cliff will the projectile strike the water?

(d) Using a graphing utility, graph the function $h$, $0\le x\le 200$.

(e) Use a graphing utility to verify the solutions found in parts (b) and (c).

(f) When the height of the projectile is 100 feet above the water, how far is it from the cliff?

To determine

To calculate:

a. At what horizontal distance from the face of the cliff is the height of the projectile a maximum?

b. Find the maximum height of the projectile?

c. At what horizontal distance from the face of the cliff will the projectile strike the water?

d. Graph the function $h$, using a graphing utility $0\le x\le 200$.

e. Using graphing utility verify the solutions found in (b) and (c).

f. When the height of the projectile is 100 feet above the water, how far is it from the cliff?

Answer to Problem 11AYU

Solution:

a. $x=39.0625$

b. $\text{219}\text{.5}$ feet.

c. 170ft.

d. The graph is given below.

e. The graph is given below.

f. $x=135.69$

Explanation of Solution

Given:

A projectile is fired from a cliff 200 feet above water at an inclination of 45degree to the horizontal, with a muzzle velocity of 50 feet per second. The height $h$ of the projectile above water is modelled by

$h(x)=\frac{-32}{{50}^2}{x}^2+x+200$, where $x$ is the horizontal distance of the projectile from the face of the cliff.

Formula used:

For a quadratic equation $f(x)=a{x}^2+bx+c,a\ne 0$, we have

$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

Calculation:

a. The height of the projectile is a quadratic equation with $a=\frac{-32}{{50}^2},b=1,c=200$. Since a is negative, the vertex is the maximum of the given function. Therefore, the maximum is ${\max }_x=\frac{-b}{2a}=\frac{-1}{2\left(\frac{-32}{{50}^2}\right)}=39.0625$.

Thus, at $x=39.0625$, the height of the projectile is maximum.

b. The maximum height of the projectile is at $h(39.0625)=\frac{-32}{{50}^2}{(39.0625)}^2+39.0625+200=219.53125$

Thus, the maximum height of the projectile is $\text{219}\text{.5}$ feet.

c. Now, we need to find the value of x at $h=0$.

$\frac{-32}{{50}^2}{x}^2+x+200=0$

\Rightarrow x=\frac{-1\pm \sqrt{{(-1)}^2-4\left(\frac{-32}{{50}^2}\right)(200)}}{2\left(\frac{-32}{{50}^2}\right)}

=170.023

The projectile will strike the water at a horizontal distance of 170ft.

d.

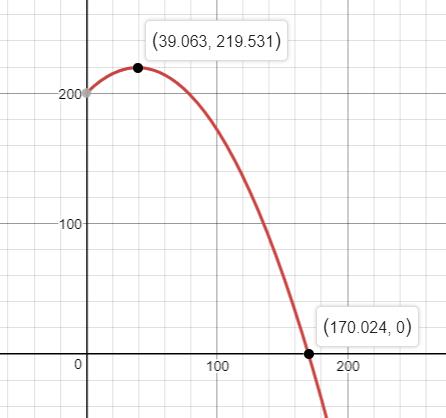
e. From the above graph, we can see that the answers in (b) and (c) are true.

f. Now, we have to find $x$ when $h=100$.

$\frac{-32}{{50}^2}{x}^2+x+200=100$

$\Rightarrow \frac{-32}{{50}^2}{x}^2+x+200-100=0$

$\Rightarrow \frac{-32}{{50}^2}{x}^2+x+100=0$

$\Rightarrow x=\frac{-1\pm \sqrt{{(-1)}^2-4\left(\frac{-32}{{50}^2}\right)(100)}}{2\left(\frac{-32}{{50}^2}\right)}=135.69$

When $h=100$, we have $x=135.69$.