Chapter 3.4, Problem 12AYU

Analyzing the Motion of a Projectile A projectile is fired at an inclination of ${45}^{\circ }$ to the horizontal, with a muzzle velocity of 100 feet per second. The height $h$ of the projectile is modeled by

$h\left(x\right)=\frac{-32x^2}{{\left(100\right)}^2}+x$

where $x$ is the horizontal distance of the projectile from the firing point.

(a) At what horizontal distance from the firing point is the height of the projectile a maximum?

(b) Find the maximum height of the projectile.

(c) At what horizontal distance from the firing point will the projectile strike the ground?

(d) Using a graphing utility, graph the function $h$ $0\le x\le 350$.

(e) Use a graphing utility to verify the results obtained in parts (b) and (c).

(f) When the height of the projectile is 50 feet above the ground, how far has it traveled horizontally?

To determine

To calculate:

At what horizontal distance from the firing point is the height of the projectile a maximum?

Find the maximum height of the projectile?

At what horizontal distance from the firing point will the projectile strike the ground?

Graph the function $h$, using a graphing utility $0\le x\le 350$.

Using graphing utility verify the solutions found in (b) and (c).

When the height of the projectile is 50 feet above the ground, how far is it travelled horizontally?

Answer to Problem 12AYU

Solution:

$x=156.25$

$78.125$ feet.

The projectile will strike the ground at a horizontal distance of $312.5$ft and at the firing point.

The graph is given below.

The graph is given below.

When $h=50$, we have $x=62.5$ and $x=250$.

Explanation of Solution

Given:

A projectile is fired from an inclination of 45 degree to the horizontal, with a muzzle velocity of 100 feet per second. The height $h$ of the projectile above water is modelled by

$h(x)=\frac{-32}{{100}^2}{x}^2+x$, where $x$ is the horizontal distance of the projectile from the firing point.

Formula used:

For a quadratic equation $f(x)=a{x}^2+bx+c,a\ne 0$, we have

$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

Calculation:

a. The height of the projectile is a quadratic equation with $a=\frac{-32}{{100}^2},b=1$. Since $a$ is negative, the vertex is the maximum of the given function. Therefore, the maximum is ${\max }_x=\frac{-b}{2a}=\frac{-1}{2\left(\frac{-32}{{100}^2}\right)}=156.25$.

Thus, at $x=156.25$, the height of the projectile is maximum.

b. The maximum height of the projectile is at $h(156.25)=\frac{-32}{{100}^2}{(156.25)}^2+156.25=78.125$

Thus, the maximum height of the projectile is $78.125$ feet.

c. Now, we need to find the value of $x$ at $h=0$.

$\frac{-32}{{100}^2}{x}^2+x=0$

\Rightarrow x=\frac{-1\pm \sqrt{{(-1)}^2-4\left(\frac{-32}{{100}^2}\right)(0)}}{2\left(\frac{-32}{{100}^2}\right)}

\Rightarrow x=0

and

x=312.5

The projectile will strike the ground at a horizontal distance of $312.5$ft and at the firing point.

d.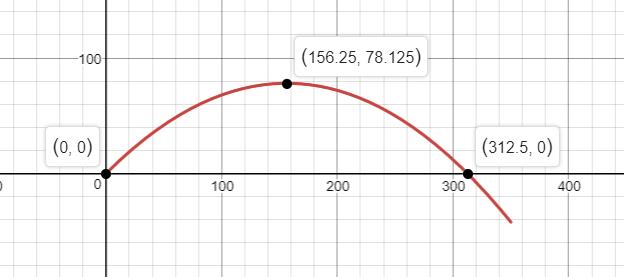

e. From the above graph, we can see that the answers in (b) and (c) are true.

f. Now, we have to find $x$ when $h=100$.

$\frac{-32}{{100}^2}{x}^2+x=50$

$\Rightarrow \frac{-32}{{100}^2}{x}^2+x-50=0$

$\Rightarrow \frac{-32}{{100}^2}{x}^2+x-50=0$

$\Rightarrow x=\frac{-1\pm \sqrt{{(-1)}^2-4\left(\frac{-32}{{100}^2}\right)(50)}}{2\left(\frac{-32}{{100}^2}\right)}$

$\Rightarrow x=62.5$

and

$x=250$

When $h=50$, we have $x=62.5$ and $x=250$.