Chapter 3.1, Problem 13AYU

In Problems 13-20, a linear function is given.

a. Determine the slope and $y\text{-intercept}$ of each Junction.

b. Use the slope and $y\text{-intercept}$ to graph the linear function.

c. Determine the average rate of change of each function.

d. Determine whether the linear function is increasing, decreasing, or constant.

$f(x)=2x+3$

To determine

To find:

(a. The Slope and the $y\text{-intercept}$ of the given function.

Answer to Problem 13AYU

Solution:

(a. The slope is 2 and $y\text{-intercept}$ is 3.

Explanation of Solution

Given:

The given equation is $f(x) = 2x + 3$.

Formula used:

For a linear function of the form $f(x)=mx+b$, $m$ is the slope and $b$ is the $y\text{-intercept}$.

The average rate of change of the linear function is the slope of that function.

The function is said to be increasing in it domain, then its slope is positive.

The function is said to be decreasing in it domain, then its slope is negative.

The function is said to be constant if the slope is 0.

Calculation:

(a. From the definition of the linear function, $f(x)=mx+b$.

Compare the given function with linear function, we get $m=2andb=3$.

The slope of the given function is 2 and 3 is the $y\text{-intercept}$.

To determine

To find:

(b. Use (a. and graph the given function.

Answer to Problem 13AYU

Solution:

(b. The graph is as shown below:

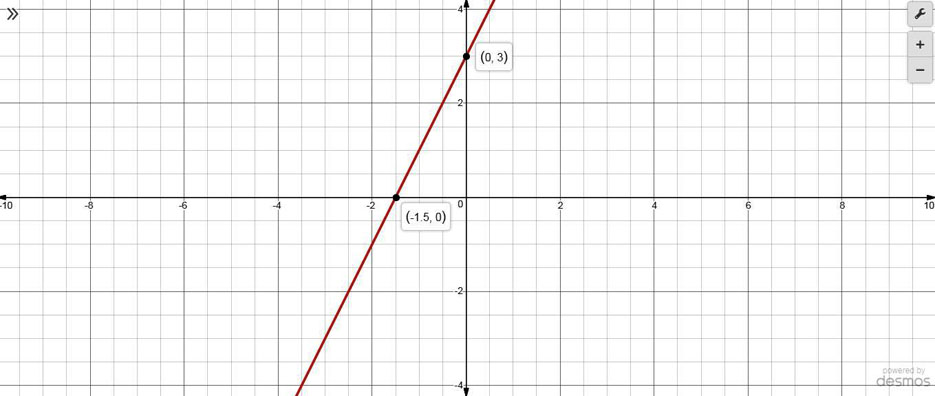
Explanation of Solution

Given:

The given equation is $f(x) = 2x + 3$.

Formula used:

For a linear function of the form $f(x)=mx+b$, $m$ is the slope and $b$ is the $y\text{-intercept}$.

The average rate of change of the linear function is the slope of that function.

The function is said to be increasing in it domain, then its slope is positive.

The function is said to be decreasing in it domain, then its slope is negative.

The function is said to be constant if the slope is 0.

Calculation:

(b. The graph of the given function is

To determine

To find:

(c. Average rate of change of the given function.

Answer to Problem 13AYU

Solution:

(c. Average rate of change of the given function is 2.

Explanation of Solution

Given:

The given equation is $f(x) = 2x + 3$.

Formula used:

For a linear function of the form $f(x)=mx+b$, $m$ is the slope and $b$ is the $y\text{-intercept}$.

The average rate of change of the linear function is the slope of that function.

The function is said to be increasing in it domain, then its slope is positive.

The function is said to be decreasing in it domain, then its slope is negative.

The function is said to be constant if the slope is 0.

Calculation:

(c.The average rate of change of the given function is 2.

To determine

To find:

(d. Determine whether the function is increasing, decreasing or constant.

Answer to Problem 13AYU

Solution:

(d. The function is increasing.

Explanation of Solution

Given:

The given equation is $f(x) = 2x + 3$.

Formula used:

For a linear function of the form $f(x)=mx+b$, $m$ is the slope and $b$ is the $y\text{-intercept}$.

The average rate of change of the linear function is the slope of that function.

The function is said to be increasing in it domain, then its slope is positive.

The function is said to be decreasing in it domain, then its slope is negative.

The function is said to be constant if the slope is 0.

Calculation:

(d. Since the slope of the given function is positive, $m > 0$. Therefore, the function is increasing.