Chapter 3.3, Problem 36AYU

In Problems 33-48, (a) graph each quadratic function by determining whether it graph opens up or down and by finding its vertex, axis of symmetry, $y\text{-intercept},\text{ and }x\text{-intercepts}$, if any. (b) Determine the domain and the range of the function. (c) Determine where the function is increasing and where it is decreasing. Verify your results using a graphing utility.

$f(x)=-x^2+4x$

To determine

To calculate:

1. To graph the given quadratic function by determining its properties.
2. Determine the domain and range of the function.
3. Determine where the function is increasing and decreasing.

Answer to Problem 36AYU

1. The graph opens downwards.

   The vertex of the given function is $(2,4)$.

   The axis of symmetry is at $x=2$.

   The $y\text{-intercepts}$ is $y=0$.

   The function has $x\text{-intercepts}$ at $x=0$ and $x=4$.

   

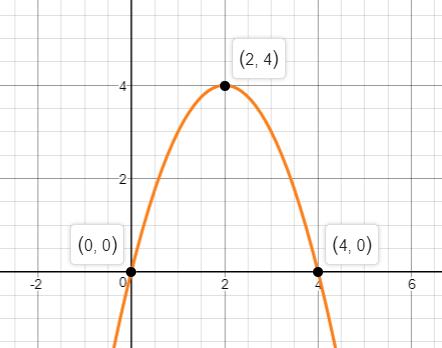
2. The domain of the given function is the set of all real numbers and the range of the given function is $(-\infty ,4]$.
3. The function is increasing in the interval $(-\infty ,2]$ and decreasing in the interval $[2,\infty )$.

Explanation of Solution

Given:

The given function is $f(x)=-x^2+4x$

Formula Used:

Consider a quadratic function $f(x)=a{x}^2+bx+c,a\ne 0$.

If $a>0$, the graph opens upwards.

If $a<0$, the graph opens downwards.

The vertex of the above function is $\left(\frac{-b}{2a},f\left(\frac{-b}{2a}\right)\right)$.

The axis of symmetry will be $x=\frac{-b}{2a}$.

We can find the $y\text{-intercept}$ by equating the equation at $x=0$.

We can find the $x\text{-intercept}$ by equating the equation at $y=0$.

Domain is the set of all possible values that $x$ can take.

Range is the possible results for any values of $x$.

Calculation:

The given function is $f(x)=-x^2+4x$.

We can see that $a=-1,b=4$ and $c=0$.

Since $a=-1$ is negative, the graph opens downwards.

We have $\frac{-b}{2a}=\frac{-4}{2(-1)}=2$ and $f\left(\frac{-b}{2a}\right)=f(-2)=-{(2)}^2+4(2)=4$

Therefore, the vertex of the given function is $(2,4)$.

The axis of symmetry is at $x=2$.

The $y\text{-intercept}$ is at $f(0)=-{(0)}^2+4(0)=0$.

Thus, the $y\text{-intercept}$ is $y=0$.

Now, we have to find the $x\text{-intercept}$.

Thus, we have

$\begin{array}{l}-x^2+4x=0\\ \Rightarrow -x(x-4)=0\\ \Rightarrow x=0\end{array}$

and

$\begin{array}{l}x-4=0\\ \Rightarrow x=4\end{array}$

Therefore, the function has $x\text{-intercept}$ at $x=0$ and $x=4$.

The graph of the given function is

The domain of the given function is the set of all real numbers. The range of the given function is $(-\infty ,4]$.

From the graph, we can see that the function is increasing in the interval $(-\infty ,2]$ and decreasing in the interval $[2,\infty )$.