Chapter 3, Problem 29RE

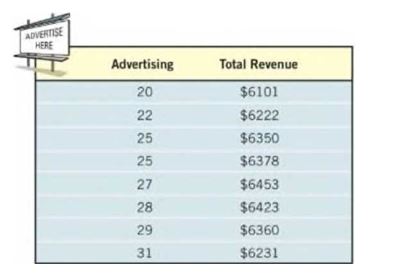
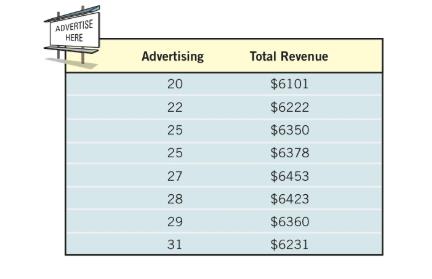
29. Advertising A small manufacturing firm collected the following data on advertising expenditures A (in thousands of dollars) and total revenue R (in thousands of dollars).

(a) Draw a scatter diagram of the data. Comment on the type of relation that may exist between the two variables.

(b) The quadratic function of best fit to these data is

$R(A) = -7.76A^2 + 411.88A+942.72$

Use this function to determine the optimal level of advertising.

(c) Use the function to predict the total revenue when the optimal level of advertising is spent.

(d) Use a graphing utility to verify that the function given in part (b) is the quadratic function of best fit.

(e) Use a graphing utility to draw a scatter diagram of the data and then graph the quadratic function of best fit on the scatter diagram.

To determine

To calculate:

1. Graph a scattered diagram and determine the type of relation that exists between the 2 variables.
2. Determine the optimum level of advertising using the given quadratic function of best fit.
3. Predict the total revenue when the optimum level of advertising is spent.
4. Use a graphing utility and verify that the given function of best fit is correct.
5. Draw the function of best fit on the scattered diagram.

Answer to Problem 29RE

Solution:

1. The graph is

   

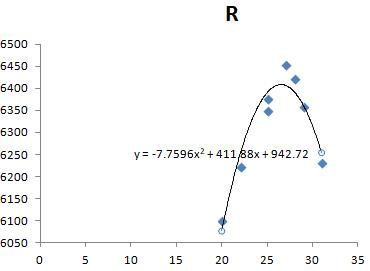
2. The optimum level of advertising is at around $\$26.5$ thousand.
3. The total revenue when the optimum level of advertising is spent is $\$6408$ thousand.
4. The given equation of best fit is true.
5. The graph is given above.

Explanation of Solution

Given:

The given data represents the relation between advertising expenditure $A$ and the total revenue $R$.

The equation of best fit is given as

$R(A)=-7.76A^2+411.88A+942.72$

Formula used:

For a quadratic function $y=a{x}^2+bx+c$, if $a$ is positive, then the vertex $\left(\frac{-b}{2a},y\left(\frac{-b}{2a}\right)\right)$ is the minimum point and if $a$ is negative, the vertex $\left(\frac{-b}{2a},y\left(\frac{-b}{2a}\right)\right)$ is the maximum point.

Calculation:

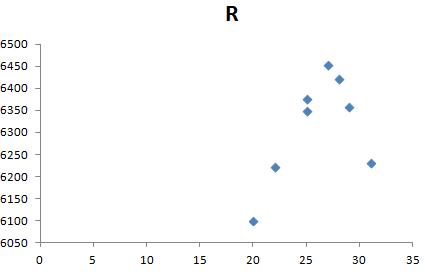
We can draw the scatter diagram using Microsoft Excel.

Thus, on entering the $x$ and the $y$ values on excel, we have to choose the Scatter diagram form the insert option.

Then for getting the equation of best fit, we have to choose the Layout option and then Trendline and then more Trendline option. Then choose the option polynomial and then display the equation.

Thus, we get the scatter diagram with the equation of best fit as

(a) The scatter diagram is drawn above and we can see that the given variables exhibit a polynomial relationship opening downwards, i.e., $a<0$.

(b) From the given quadratic equation, we can get that

$\frac{-b}{2a}=\frac{-411.88}{2(-7.76)}=26.54$

Thus, the optimum level of advertising is at around $\$26.5$ thousand.

(c) When $A=26.5$, the total revenue will be

$R(26.5)=-7.76{(26.5)}^2+411.88(26.5)+942.72=6408$

The total revenue when the optimum level of advertising is spent is $\$6408$ thousand.

(d) Using a graphing utility, we get the equation of best fit as $R(A)=-7.76A^2+411.88A+942.72$

Thus, the given equation of best fit is correct.