Chapter 3, Problem 5CT

In Problems 4 and 5,

a. Determine whether the graph opens up or down.

b. Determine the vertex of the graph of the quadratic function.

c. Determine the axis of symmetry of the graph of the quadratic function.

d. Determine the intercepts of the graph of the quadratic function.

e. Use the information in parts (a)-(d) to graph the quadratic function.

f. Based on the graph, determine the domain and the range of the quadratic function.

g. Based on the graph, determine where the function is increasing and where it is decreasing.

$g(x)=-2x^2+4x-5$

To determine

To calculate:

1. Whether the graph opens upwards or downwards?
2. Determine the vertex of the function.
3. Determine the axis of symmetry.
4. Determine the intercepts of the graph of the given function.
5. Graph the given function.
6. Determine the domain and range of the function.
7. Determine where the function is increasing and where it is decreasing.

Answer to Problem 5CT

Solution:

a. The graph opens down as $a$ is negative.

b. The vertex is at $(1,-3)$.

c. The axis of symmetry is the vertical line $x=1$.

d. The intercepts of the given function is $\frac{-4\pm \sqrt{16-40}}{-4}$.

e. Graph of the given function is

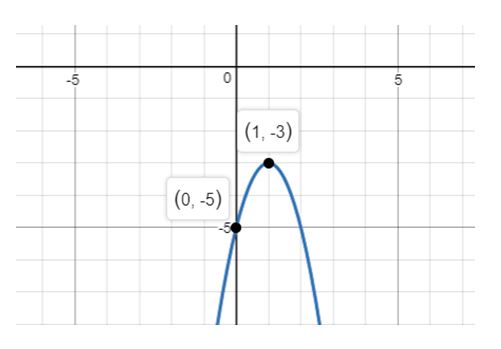
f. The domain of the function is $(-\infty ,\infty )$ and range is $(-\infty ,-3)$.

g. The function is increasing in the interval $(-\infty ,1)$ and is decreasing in the interval $(1,\infty )$.

Explanation of Solution

Given:

The given function is $g(x)=-2x^2+4x-5$

Formula used:

Consider the function $f(x)=a{x}^2+bx+c,a\ne 0$.

The vertex is at $\left(\frac{-b}{2a},f\left(\frac{-b}{2a}\right)\right)$.

The axis of symmetry is the vertical line $x=\frac{-b}{2a}$.

If $a>0$, then the graph opens up and the vertex is the minimum point.

If $a<0$, then the graph opens downwards and the vertex is the maximum point.

The $x\text{-intercept}$ is obtained by substituting $y=0$ in the given equation.

The $y\text{-intercept}$ is obtained by substituting $x=0$ in the given equation.

Calculation:

The given function is a quadratic function with $a=-2,b=4,c=-5$.

a. The graph opens down as $a$ is negative.

b. The vertex is at

$\frac{-b}{2a}=\frac{-(4)}{2(-2)}=1$

$f\left(1\right)=-2{\left(1\right)}^2+4(1)-5=-3$

$\Rightarrow \left(\frac{-b}{2a},f\left(\frac{-b}{2a}\right)\right)=(1,-3)$

Thus, the vertex is at $(1,-3)$.

c. The axis of symmetry is the vertical line $x=1$.

d. Determine the intercepts of the graph of the given function.

When $x=0$, we get the $y\text{-intercept}$ as

$g(0)=-2{(0)}^2+4(0)-5=-5$

Thus, the $y\text{-intercept}$ is at $y=-5$.

When $y=0$, we get the $x\text{-intercepts}$ as

$-2x^2+4x-5=0$

$\Rightarrow x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}=\frac{-(4)\pm \sqrt{{(4)}^2-4(-2)(-5)}}{2(-2)}$

$=\frac{-4\pm \sqrt{16-40}}{-4}$

Here, we can see at $y=0$, the value of $x$ is going imaginary.

Thus, there are no $x\text{-intercepts}$.

e. Graph of the given function is

f. The domain of the function is $(-\infty ,\infty )$ and range is $(-\infty ,-3)$.

g. The function is increasing in the interval $(-\infty ,1)$ and is decreasing in the interval $(1,\infty )$.