Introduction to Heat Transfer
6th Edition
ISBN: 9780470501962
Author: Frank P. Incropera, David P. DeWitt, Theodore L. Bergman, Adrienne S. Lavine
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 4, Problem 4.2P
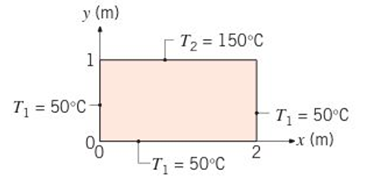
A two-dimensional rectangular plate is subjected to prescribedboundary conditions. Using the results of the exactsolution for the heat equation presented in Section 4.2,calculate the temperature at the midpoint
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
T1=68
T2=43
Q3:
Q1
Passage of an electric current through a long conducting
rod of radius r; and thermal conductivity k, results in
uniform volumetric heating at a rate of ġ. The conduct-
ing rod is wrapped in an electrically nonconducting
cladding material of outer radius r, and thermal conduc-
tivity k, and convection cooling is provided by an
adjoining fluid.
Conducting
rod, ġ, k,
11
To
Čladding, ke
For steady-state conditions, write appropriate forms of
the heat equations for the rod and cladding. Express ap-
propriate boundary conditions for the solution of these
equations.
Please show all work for this mechnical measure problem. Not Ai generated the answers have been wrong I need to understand.
Chapter 4 Solutions
Introduction to Heat Transfer
Ch. 4 - In the method of separation of variables (Section...Ch. 4 - A two-dimensional rectangular plate is subjected...Ch. 4 - Consider the two-dimensional rectangular plate...Ch. 4 - A two-dimensional rectangular plate is subjected...Ch. 4 - Prob. 4.5PCh. 4 - Prob. 4.6PCh. 4 - Free convection heat transfer is sometimes...Ch. 4 - Prob. 4.8PCh. 4 - Radioactive wastes are temporarily stored in a...Ch. 4 - Based on the dimensionless conduction heat rates...
Ch. 4 - Prob. 4.11PCh. 4 - A two-dimensional object is subjected to...Ch. 4 - Prob. 4.13PCh. 4 - Two parallel pipelines spaced 0.5 m apart are...Ch. 4 - A small water droplet of diameter D=100m and...Ch. 4 - Prob. 4.16PCh. 4 - Pressurized steam at 450 K flows through a long,...Ch. 4 - Prob. 4.19PCh. 4 - A furnace of cubical shape, with external...Ch. 4 - Prob. 4.21PCh. 4 - Prob. 4.22PCh. 4 - A pipeline, used for the transport of crude oil,...Ch. 4 - A long power transmission cable is buried at a...Ch. 4 - Prob. 4.25PCh. 4 - A cubical glass melting furnace has exterior...Ch. 4 - Prob. 4.27PCh. 4 - An aluminum heat sink k=240W/mK, used to coolan...Ch. 4 - Hot water is transported from a cogeneration power...Ch. 4 - Prob. 4.30PCh. 4 - Prob. 4.31PCh. 4 - Prob. 4.32PCh. 4 - An igloo is built in the shape of a hemisphere,...Ch. 4 - Consider the thin integrated circuit (chip) of...Ch. 4 - Prob. 4.35PCh. 4 - The elemental unit of an air heater consists of a...Ch. 4 - Prob. 4.37PCh. 4 - Prob. 4.38PCh. 4 - Prob. 4.39PCh. 4 - Prob. 4.40PCh. 4 - Prob. 4.41PCh. 4 - Determine expressions for...Ch. 4 - Prob. 4.43PCh. 4 - Prob. 4.44PCh. 4 - Prob. 4.45PCh. 4 - Derive the nodal finite-difference equations for...Ch. 4 - Prob. 4.47PCh. 4 - Prob. 4.48PCh. 4 - Consider a one-dimensional fin of uniform...Ch. 4 - Prob. 4.50PCh. 4 - Prob. 4.52PCh. 4 - Prob. 4.53PCh. 4 - Prob. 4.54PCh. 4 - Prob. 4.55PCh. 4 - Prob. 4.56PCh. 4 - Steady-state temperatures at selected nodal points...Ch. 4 - Prob. 4.58PCh. 4 - Prob. 4.60PCh. 4 - The steady-state temperatures C associated with...Ch. 4 - A steady-state, finite-difference analysis has...Ch. 4 - Prob. 4.64PCh. 4 - Consider a long bar of square cross section (0.8 m...Ch. 4 - Prob. 4.66PCh. 4 - Prob. 4.67PCh. 4 - Prob. 4.68PCh. 4 - Prob. 4.69PCh. 4 - Consider Problem 4.69. An engineer desires to...Ch. 4 - Consider using the experimental methodology of...Ch. 4 - Prob. 4.72PCh. 4 - Prob. 4.73PCh. 4 - Prob. 4.74PCh. 4 - Prob. 4.75PCh. 4 - Prob. 4.76PCh. 4 - Prob. 4.77PCh. 4 - Prob. 4.78PCh. 4 - Prob. 4.79PCh. 4 - Prob. 4.80PCh. 4 - Spheres A and B arc initially at 800 K, and they...Ch. 4 - Spheres of 40-mm diameter heated to a uniform...Ch. 4 - To determine which parts of a spiders brain are...Ch. 4 - Prob. 4.84P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- The subject is Mechanics of Deformable Bodiesarrow_forwardA 1-D conduction heat transfer problem with internal energy generation is governed by the following equation: +-= dx2 =0 W where è = 5E5 and k = 32 If you are given the following node diagram with a spacing of Ax = .02m and know that m-K T = 611K and T, = 600K, write the general equation for these internal nodes in finite difference form and determine the temperature at nodes 3 and 4. Insulated Ar , T For the answer window, enter the temperature at node 4 in Kelvin (K). Your Answer: EN SORN Answer units Pri qu) 232 PM 4/27/2022 99+ 66°F Sunny a . 20 ENLARGED oW TEXTURE PRT SCR IOS DEL F8 F10 F12 BACKSPACE num - %3D LOCK HOME PGUP 170arrow_forwardPlease answer the question with explicit scheme and calculation is done until the second time!arrow_forward
- Let an aluminum rod of length 20 cm be initially at the uniform temperature of 25° C. Suppose that at time t = 0, the end x = 0 is cooled to 0° C while the end x = 20 is heated to 60° C, and both are thereafter maintained at those temperatures. (a) Find the temperature distribution in the rod at any time t.arrow_forwardA wall of a house is made from two layers of bricks enclosing a layer of insulation. A radiator is positioned to cover the whole internal surface, and used intermittently when the internal temperature is low. The external surface is exposed to the outside air. Which of the following assumptions could be used to identify the relevant reduced form of the conduction equation to find the temperature in the wall. a. Conduction is mainly in two directions. b. Conduction is mainly in one direction. c. The wall properties are homogeneous. d. Steady conditions exist. e. Unsteady conditions exist. f. There is an internal volumetric heat generation in the wall.arrow_forward2. A slab of thickness Lis initially at zero temperature. For times t> 0, the boundary surface at x 0 is subjected to a time-dependent prescribed temperature f(t) defined by: a + bt for 0Ti and the boundary at x = L is kept insulated. Using Duhamel's theorem, develop an expression for the temperature distribution in the slab for times (i) t t1.arrow_forward
- i need the answer quicklyarrow_forwardThe initial temperature distribution of a 5 cm long stick is given by the following function. The circumference of the rod in question is completely insulated, but both ends are kept at a temperature of 0 °C. Obtain the heat conduction along the rod as a function of time and position ? (x = 1.752 cm²/s for the bar in question) 100 A) T(x1) = 1 Sin ().e(-1,752 (³¹)+(sin().e (-1,752 (²) ₁ + 1 3π TC3 .....) 100 t + ··· ....... 13) T(x,t) = 200 Sin ().e(-1,752 (²t) + (sin (3). e (-1,752 (7) ²) t B) 3/3 t + …............) C) T(x.t) = 200 Sin ().e(-1,752 (²t) (sin().e(-1,752 (7) ²) t – D) T(x,t) = 200 Sin ().e(-1,752 (²)-(sin().e (-1,752 (²7) ²) t E) T(x.t)=(Sin().e(-1,752 (²t)-(sin().e(-1,752 (²) t+ t + ··· .........) t +.... t + ··· .........) …..)arrow_forwardi need the answer quicklyarrow_forward
- Find the two-dimensional temperature distribution T(x,y) and midplane temperature T(B/2,W/2) under steady state condition. The density, conductivity and specific heat of the material are p=(1200*32)kg/mº, k=400 W/m.K, and cp=2500 J/kg.K, respectively. A uniform heat flux 9" =1000 W/m² is applied to the upper surface. The right and left surfaces are also kept at 0°C. Bottom surface is insulated. 9" (W/m) T=0°C T=0°C W=(10*32)cm B=(30*32)cmarrow_forwardSuppose that a finite-difference solution has been obtained for the temperature T, near but not at an adiabatic boundary. in most instances, it would be necessary or desirable to evaluate the temperature at the boundary point itself. for this case of an adiabatic boundary, develop an expression for the temperature at the boundary T1, in the terms of temperatures at neighbouring points T2, T3, etc, by assuming that the temperature distribution in the neighbourhood of the boundary is a straight line a second-degree polynomial a cubic polynomial (you only need to indicate how you would derive this one) indicate the order of T.E in each of the above approximations used to evaluate T1arrow_forward2. The slab shown is embedded in insulating materials on five sides, while the front face experiences convection off its face. Heat is generated inside the material by an exothermic reaction equal to 1.0 kW/m'. The thermal conductivity of the slab is 0.2 W/mk. a. Simplify the heat conduction equation and integrate the resulting ID steady form of to find the temperature distribution of the slab, T(x). b. Present the temperature of the front and back faces of the slab. n-20- 10 cm IT- 25°C) 100 cm 100 cmarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Heat Transfer – Conduction, Convection and Radiation; Author: NG Science;https://www.youtube.com/watch?v=Me60Ti0E_rY;License: Standard youtube license