
Concept explainers
22. Installing Cable TV MetroMedia Cable is asked to provide service to a customer whose house is located 2 miles from the road along which the cable is buried. The nearest connection box for the cable is located 5 miles down the road. See the figure.
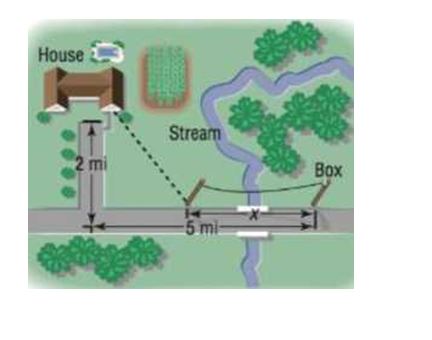
(a) If the installation cost is S500 per mile along the road and per mile off the road, build a model that expresses the total cost C of installation as a function of the distance x (in miles) from the connection box to the point where the cable installation turns off the road. Find the domain of .
(b) Compute the cost if mile.
(c) Compute the cost if miles.
(d) Graph the function . Use TRACE to see how the cost C varies as x changes from 0 to 5.
(e) What value of x results in the least cost?
To find:
a. To model that expresses the total cost of installation as a function of distance . To find the domain of .
Answer to Problem 22AYU
Solution:
a. .
Explanation of Solution
Given:
1. The house is 2 miles from the road.
2. The nearest connection box is 5 miles down the road.
3. Cost of installation is per mile along the road and per off the road.
Calculation:
The can be expressed as the figure below.
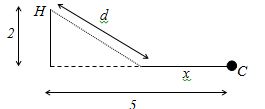
Let be the distance along the road.
Let be the distance off the road.
a. The total cost of installation
From the figure, .
The Cost of installation .
To find:
b. To compute the cost if mile.
Answer to Problem 22AYU
Solution:
b. .
Explanation of Solution
Given:
1. The house is 2 miles from the road.
2. The nearest connection box is 5 miles down the road.
3. Cost of installation is per mile along the road and per off the road.
Calculation:
The can be expressed as the figure below.

Let be the distance along the road.
Let be the distance off the road.
b. For
To find:
c. To compute the cost if miles.
Answer to Problem 22AYU
Solution:
c.
Explanation of Solution
Given:
1. The house is 2 miles from the road.
2. The nearest connection box is 5 miles down the road.
3. Cost of installation is per mile along the road and per off the road.
Calculation:
The can be expressed as the figure below.

Let be the distance along the road.
Let be the distance off the road.
c. For .
To find:
d. To graph the function .
Answer to Problem 22AYU
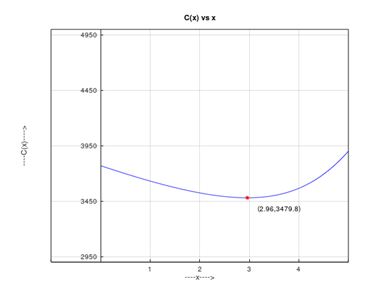
Explanation of Solution
Given:
1. The house is 2 miles from the road.
2. The nearest connection box is 5 miles down the road.
3. Cost of installation is per mile along the road and per off the road.
Calculation:
The can be expressed as the figure below.

Let be the distance along the road.
Let be the distance off the road.
d. To graph :

| Sl No | In miles | In |
|---|---|---|
| 1. | 0 | |
| 2 | 1 | |
| 3 | 2 | |
| 4 | 3 | |
| 5 | 4 | |
| 6 | 5 |
To find:
e. To find the value of in which the cost is least..
Answer to Problem 22AYU
Solution:
e. .
Explanation of Solution
Given:
1. The house is 2 miles from the road.
2. The nearest connection box is 5 miles down the road.
3. Cost of installation is per mile along the road and per off the road.
Calculation:
The can be expressed as the figure below.

Let be the distance along the road.
Let be the distance off the road.
e. The value of is least when miles.
Chapter 2 Solutions
Precalculus
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
Calculus: Early Transcendentals (2nd Edition)
College Algebra (7th Edition)
Elementary Statistics
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
- Math 2 question. thxarrow_forwardPlease help on this Math 1arrow_forward2. (5 points) Let f(x) = = - - - x² − 3x+7. Find the local minimum and maximum point(s) of f(x), and write them in the form (a, b), specifying whether each point is a minimum or maximum. Coordinates should be kept in fractions. Additionally, provide in your answer if f(x) has an absolute minimum or maximum over its entire domain with their corresponding values. Otherwise, state that there is no absolute maximum or minimum. As a reminder, ∞ and -∞ are not considered absolute maxima and minima respectively.arrow_forward
- Let h(x, y, z) = — In (x) — z y7-4z - y4 + 3x²z — e²xy ln(z) + 10y²z. (a) Holding all other variables constant, take the partial derivative of h(x, y, z) with respect to x, 2 h(x, y, z). მ (b) Holding all other variables constant, take the partial derivative of h(x, y, z) with respect to y, 2 h(x, y, z).arrow_forwardmath help plzarrow_forwardYou guys solved for the wrong answer. The answer in the box is incorrect help me solve for the right one.arrow_forward
- Please help me solve.arrow_forwardj) f) lim x+x ex g) lim Inx h) lim x-5 i) lim arctan x x700 lim arctanx 811xarrow_forward4. Evaluate the following integrals. Show your work. a) -x b) f₁²x²/2 + x² dx c) fe³xdx d) [2 cos(5x) dx e) √ 35x6 3+5x7 dx 3 g) reve √ dt h) fx (x-5) 10 dx dt 1+12arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





