Chapter 2.5, Problem 77AYU

(a)

To determine

To find: the temperature which is thermostat set during daytime hours and to find the temperature which is the thermostat set overnight.

Answer to Problem 77AYU

The best match is (II)

Explanation of Solution

Given information:

Energy conservation experts estimate that homeowners can save 5% to 19% on winter heating bils by programming their thermostats 5 to 10 degrees lower while sleeping. In the given graph, the temperature $T$ of a home is given as a function of time $t$ over a 24 hour period.

  

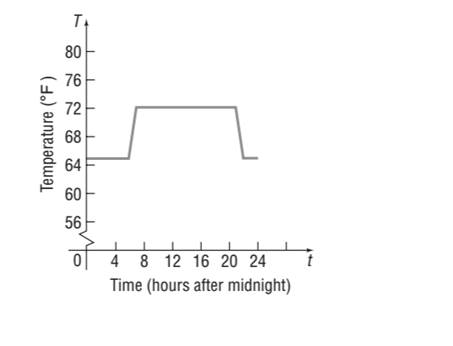
Calculation:

From the given graph, it can be seen that during the daytime hours, 8 to 20 hours after, the thermostat is set to $72°F$ .

We can see that overnight, time before and after the hours 8 and 20, the thermostat is set to $65°F$ .

(b)

To determine

To find: how thermostat affects the temperature in the house, and to graph this new function.

Answer to Problem 77AYU

The temperature decreases to $70°F$ and during the night it becomes $63°F$ .

Explanation of Solution

Given information:

Energy conservation experts estimate that homeowners can save 5% to 19% on winter heating bils by programming their thermostats 5 to 10 degrees lower while sleeping. In the given graph, the temperature $T$ of a home is given as a function of time $t$ over a 24 hour period.

  

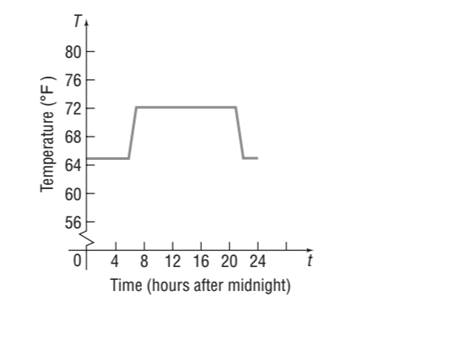
The homeowner reprograms the thermostat to $y=T\left(t\right)-2$ .

Calculation:

The graph of the function, $y=T\left(t\right)-2$ , is obtained by vertically shifting down the given graph by 2 units.

  

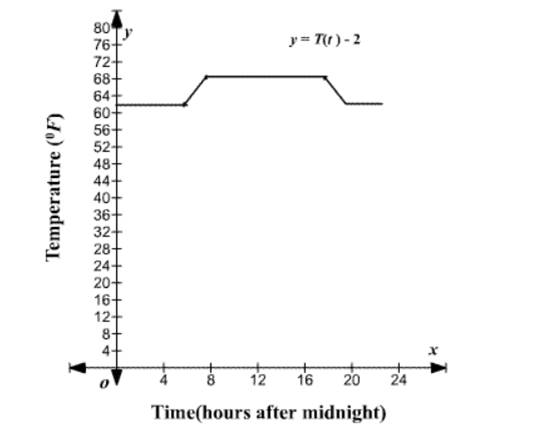
The temperature in the house will decrease by 2 degrees. During the daytime hours, the temperature decreases to $70°F$ and during the night it becomes $63°F$ .

(c)

To determine

To find: how thermostat affects the temperature in the house, and to graph this new function.

Answer to Problem 77AYU

The thermostat starts warming up at instead of and cools down from instead of.

Explanation of Solution

Given information:

Energy conservation experts estimate that homeowners can save 5% to 19% on winter heating bils by programming their thermostats 5 to 10 degrees lower while sleeping. In the given graph, the temperature $T$ of a home is given as a function of time $t$ over a 24 hour period.

  

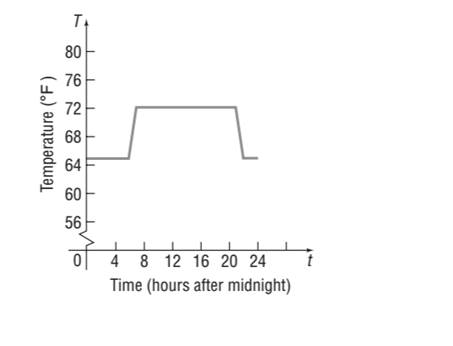
The homeowner reprograms the thermostat to $y=T\left(t+1\right)$ .

Calculation:

The graph of the function, $y=T\left(t+1\right)$ , is obtained by vertically shifting down the given graph by 1 units.

  

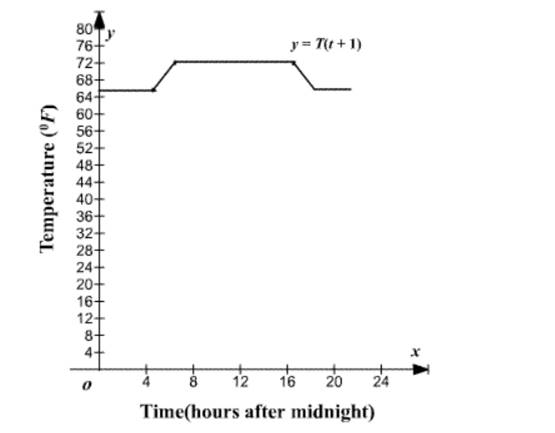
We can see that the temperature remains the same, but the daytime and overmight setting change to 1 hour earlier. That is the thermostat starts warming up at instead of and cools down from instead of.