Chapter 2.2, Problem 43AYU

(a)

To determine

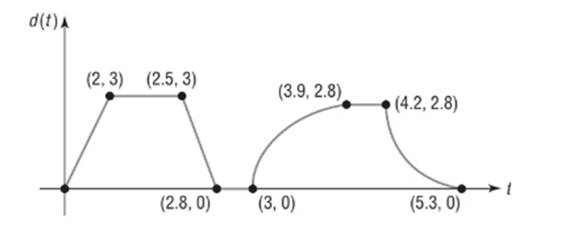
To find: the number of hours elapsed and to find the distance K from home during time.

Answer to Problem 43AYU

2 hours elapsed.

K was between 0 and 3 miles from home.

Explanation of Solution

Given information:

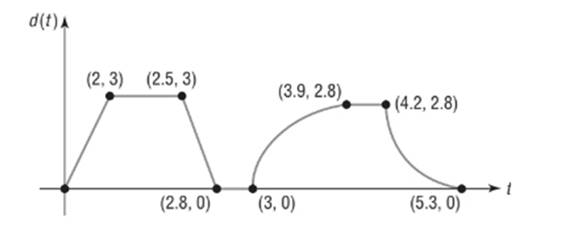
The sketch represents the distance $d$ that K was from home as a function of time $t$ .

  

From $t=0\text{to}t=2$

Calculation:

From the graph we see $\left(2-0\right)=2$ hours elapsed.

During this period K was between 0 and 3 miles from home.

(b)

To determine

To find: the number of hours elapsed and to find the distance K from home during time.

Answer to Problem 43AYU

0.5 hours elapsed.

K was between 3 miles from home.

Explanation of Solution

Given information:

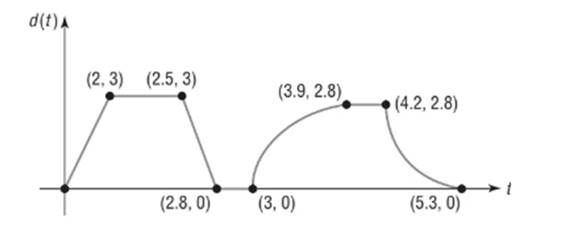
The sketch represents the distance $d$ that K was from home as a function of time $t$ .

  

From $t=2\text{to}t=2.5$

Calculation:

From the graph we see $\left(2.5-2\right)=0.5$ hours elapsed.

During this period K was 3 miles from home.

(c)

To determine

To find: the number of hours elapsed and to find the distance K from home during time.

Answer to Problem 43AYU

0.3 hours elapsed.

K was between 0 and 3 miles from home.

Explanation of Solution

Given information:

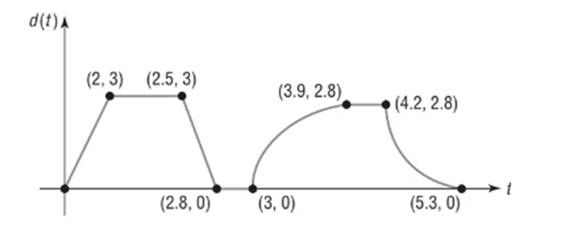
The sketch represents the distance $d$ that K was from home as a function of time $t$ .

  

From $t=2.5\text{to}t=2.8$

Calculation:

From the graph we see $\left(2.8-2.5\right)=0.3$ hours elapsed.

During this period K was between 0 and 3 miles from home.

(d)

To determine

To find: the number of hours elapsed and to find the distance K from home during time.

Answer to Problem 43AYU

0.2 hours elapsed.

K was 0 miles from home.

Explanation of Solution

Given information:

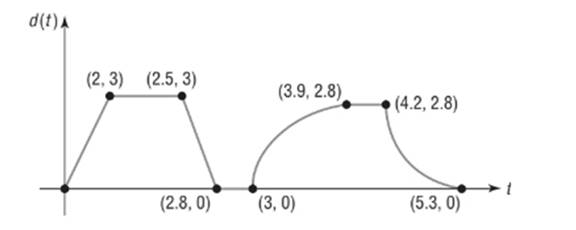
The sketch represents the distance $d$ that K was from home as a function of time $t$ .

  

From $t=2.8\text{to}t=3$

Calculation:

From the graph we see $\left(3-2.8\right)=0.2$ hours elapsed.

During this period K was 0 miles from home.

(e)

To determine

To find: the number of hours elapsed and to find the distance K from home during time.

Answer to Problem 43AYU

0.9 hours elapsed.

K was between 0 and 2.8 miles from home.

Explanation of Solution

Given information:

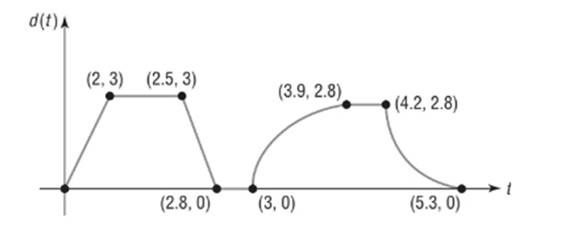
The sketch represents the distance $d$ that K was from home as a function of time $t$ .

  

From $t=3\text{to}t=3.9$

Calculation:

From the graph we see $\left(3.9-3\right)=0.9$ hours elapsed.

During this period K was between 0 and 2.8 miles from home.

(f)

To determine

To find: the number of hours elapsed and to find the distance K from home during time.

Answer to Problem 43AYU

0.3 hours elapsed.

K was 2.8 miles from home.

Explanation of Solution

Given information:

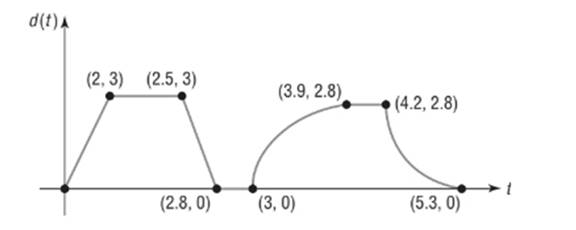
The sketch represents the distance $d$ that K was from home as a function of time $t$ .

  

From $t=3.9\text{to}t=4.2$

Calculation:

From the graph we see $\left(4.2-3.9\right)=0.3$ hours elapsed.

During this period K was 2.8 miles from home.

(g)

To determine

To find: the number of hours elapsed and to find the distance K from home during time.

Answer to Problem 43AYU

1.1 hours elapsed.

K was between 0 and 2.8 miles from home.

Explanation of Solution

Given information:

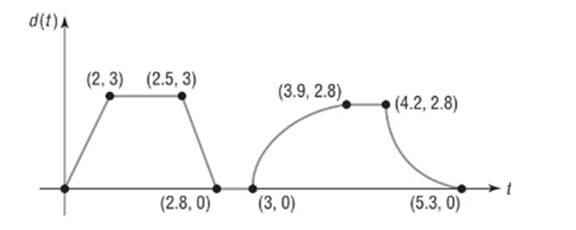
The sketch represents the distance $d$ that K was from home as a function of time $t$ .

  

From $t=4.2\text{to}t=5.3$

Calculation:

From the graph we see $\left(5.3-4.2\right)=1.1$ hours elapsed.

During this period K was between 0 and 2.8 miles from home.

(h)

To determine

To find: the farthest distance that K was from home.

Answer to Problem 43AYU

The farthest distance from home is 3 miles.

Explanation of Solution

Given information:

The sketch represents the distance $d$ that K was from home as a function of time $t$ .

  

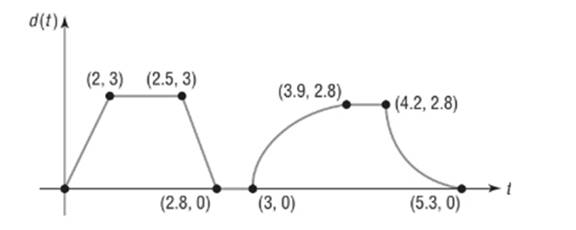
Calculation:

From the graph we see the maximum value of distance from home $d\left(t\right)$ occurs between 2 and 2.5 hours.

So the farthest distance from home is 3 miles.

(i)

To determine

To find: the number of times K did return home.

Answer to Problem 43AYU

The answer is 2 times.

Explanation of Solution

Given information:

The sketch represents the distance $d$ that K was from home as a function of time $t$ .

  

Calculation:

From the graph we see at $t=0,2.8,3,5.3$ hours the distance from home is 0.

At $t=2.8$ and $t=5.3$ he returned home. So the answer is 2 times.