Chapter 2.3, Problem 78AYU

National Debt The size of the total debt owed by the United States federal government continues to grow. In fact, according to the Department of the Treasury, the debt per person living in the United States is approximately $\$63,720$(or over $\$172,000$ per U.S. household). The following data represent the U.S. debt for the years $2007-2017$. Since the debt $D$ depends on the year $y,$ and each input corresponds to exactly one output, the debt is a function of the year. So $D(y)$ represents the debt for each year $y.$

$\begin{array}{cc}\text{Year}& \text{Debt(billions}\text{of}\text{dollars)}\\ 2007& 9008\\ 2008& 10,025\\ 2009& 11,910\\ 2010& 13,562\\ 2011& 14,790\\ 2012& 16,066\\ 2013& 16,738\\ 2014& 17,824\\ 2015& 18,151\\ 2016& 19,573\\ 2017& 20,245\end{array}$

Plot the points $(2007,9008),(2008,10025)$, and so on.

Draw a line segment from the point $(2007,9008)$ to $(2012,16066)$. What does the slope of this line segment represent?

Find the average rate of change of the debt from $2008$ to $2010$.

Find the average rate of change of the debt from $2011$ to $2013$.

Find the average rate of change of the debt from $2014$ to $2016$.

What appears to be happening to the average rate of change as time passes?

To determine

To graph: The points $\left(2007,9008\right),\left(2008,10025\right)$ and so on. Where the following data represents the U.S debt for the years $2007-2017$, and the debt is a function $D\left(y\right)$ for each year $y$:

$\begin{array}{cc}& \text{Debt}\\ \text{Year}& \left(\text{billions}\text{of}\text{dollars}\right)\\ 2007& 9008\\ 2008& 10,025\\ 2009& 11,910\\ 2010& 13,562\\ 2011& 14,790\\ 2012& 16,066\\ 2013& 16,738\\ 2014& 17,824\\ 2015& 18,151\\ 2016& 19,573\\ 2017& 20,245\end{array}$

Explanation of Solution

Given Information:

The following data represents the U.S debt for the years $2007-2017$, and the debt is a function $D\left(y\right)$ for each year $y$:

$\begin{array}{cc}& \text{Debt}\\ \text{Year}& \left(\text{billions}\text{of}\text{dollars}\right)\\ 2007& 9008\\ 2008& 10,025\\ 2009& 11,910\\ 2010& 13,562\\ 2011& 14,790\\ 2012& 16,066\\ 2013& 16,738\\ 2014& 17,824\\ 2015& 18,151\\ 2016& 19,573\\ 2017& 20,245\end{array}$

Graph:

To plot the points $\left(2007,9008\right),\left(2008,10,025\right),\left(2009,11,910\right)$ and so on, the $x$-axis shows the years after two thousands, and the $y$- axis shows the debt function in each year in thousands billions of dollars.

The point $\left(2007,9008\right)$ represents the debt $9008$ billions of dollars for year $2007$.

Similarly, all the remaining points represent the debt in billions of dollars for each year from $2008-2017$.

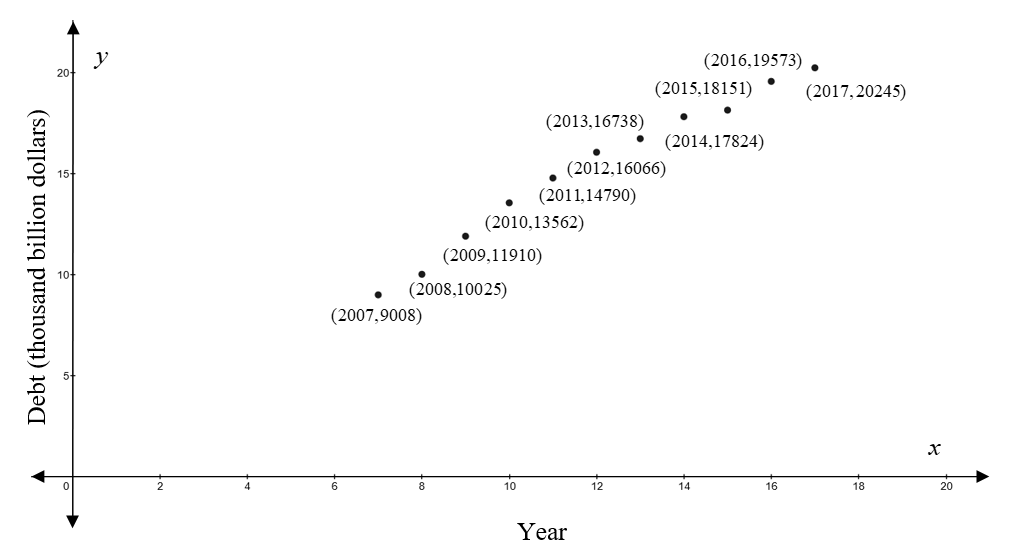
Interpretation:

The graph shows that the cost of U.S. debt increases each year from $2007-2017$.

To determine

To graph: The line segment from the points $\left(2007,9008\right)$ to $\left(2012,16066\right)$, and interpret the slope of line the segment represents. Where the following data represents the U.S debt for the years $2007-2017$, and the debt is a function $D\left(y\right)$ for each year $y$:

$\begin{array}{cc}& \text{Debt}\\ \text{Year}& \left(\text{billions}\text{of}\text{dollars}\right)\\ 2007& 9008\\ 2008& 10,025\\ 2009& 11,910\\ 2010& 13,562\\ 2011& 14,790\\ 2012& 16,066\\ 2013& 16,738\\ 2014& 17,824\\ 2015& 18,151\\ 2016& 19,573\\ 2017& 20,245\end{array}$

Explanation of Solution

Given Information:

The following data represents the U.S. debt for the years $2007-2017$ and the debt is a function $D\left(y\right)$ for each year $y$:

$\begin{array}{cc}& \text{Debt}\\ \text{Year}& \left(\text{billions}\text{of}\text{dollars}\right)\\ 2007& 9008\\ 2008& 10,025\\ 2009& 11,910\\ 2010& 13,562\\ 2011& 14,790\\ 2012& 16,066\\ 2013& 16,738\\ 2014& 17,824\\ 2015& 18,151\\ 2016& 19,573\\ 2017& 20,245\end{array}$

Graph:

The $x$-axis shows the years aftertwo thousand, and the $y$- axis shows the debt function in each year in thousand billions of dollars.

The point $\left(2007,9008\right)$ represents the debt $9008$ billions of dollars for year $2007$.

Similarly, the point $\left(2012,16066\right)$ represents the debt $16066$ billions of dollars for year $2012$.

To draw the line segment from $\left(2007,9008\right)$ to $\left(2012,16066\right)$,

First, find the slope of line segment passing though the points $\left(2007,9008\right)$ to $\left(2012,16066\right)$ by using the slope formula, $m=\frac{y_2-y_1}{x_2-x_1}$.

Here, $y_2=16066,y_1=9008,x_1=2007$ and $x_2=2012$.

$\Rightarrow m=\frac{16066-9008}{2012-2007}$

$=\frac{7058}{5}$

$=1411.6$

Therefore, slope of line segment from point $\left(2007,9008\right)$ to $\left(2012,16066\right)$ is $\$1411.6$ billion per year.

To draw the line segment, first find the equation of line by using the point-slope formula,

$y-y_1=m\left(x-x_1\right)$.

Here, $y_1=9008$, and $x_1=2007$.

Therefore,

$\Rightarrow y-9008=1411.6\left(x-2007\right)$

$\Rightarrow y-9008=1411.6x-2833081.2$

$\Rightarrow y=540x-2824073.2$

The line segment from the points $\left(2007,9008\right)$ to $\left(2012,16066\right)$ is as shown below:

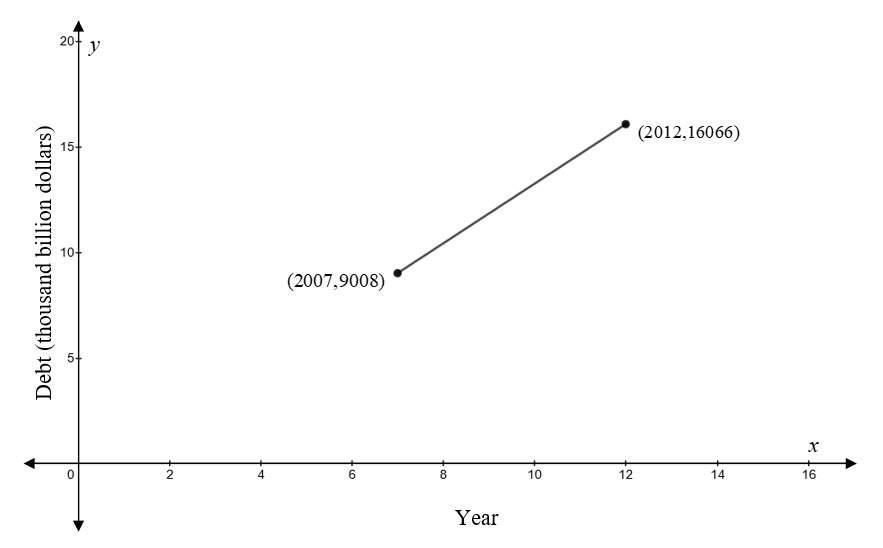
That means the slope of line segment from point $\left(2007,9008\right)$ to $\left(2012,16066\right)$ is increasing.

That is, the debt in U.S. increases from year $2007-2012$.

Interpretation:

The slope of the line segment from point $\left(2007,9008\right)$ to $\left(2012,16066\right)$ is increasing. That means the debt in U.S. is increasing from year $2007-2012$.

To determine

To calculate: The average rate of change of the debt fromyear $2008-2010$.

Answer to Problem 78AYU

Solution:

The average rate of change of the debt from $2008-2010$ is $\$1768.5$ billion per year.

Explanation of Solution

Given Information:

The following data represents the U.S debt for the years $2007-2017$, and the debt is a function $D\left(y\right)$ for each year $y$:

$\begin{array}{cc}& \text{Debt}\\ \text{Year}& \left(\text{billions}\text{of}\text{dollars}\right)\\ 2007& 9008\\ 2008& 10,025\\ 2009& 11,910\\ 2010& 13,562\\ 2011& 14,790\\ 2012& 16,066\\ 2013& 16,738\\ 2014& 17,824\\ 2015& 18,151\\ 2016& 19,573\\ 2017& 20,245\end{array}$

Formula used:

The average rate of change of function $y=f\left(x\right)$ from $a$ to $b$ is defined as:

Average rate of change $=\frac{\Delta y}{\Delta x}=\frac{f\left(b\right)-f\left(a\right)}{b-a}$ where $a$ and $b$, $a\ne b$, are in the domain of $f\left(x\right)$.

Calculation:

The average rate of change of the debt from $2008-2010$ is

$\text{Average}\text{rate}\text{of}\text{change}=\frac{\Delta y}{\Delta x}=\frac{D\left(2010\right)-D\left(2008\right)}{2010-2008}$.

From the table, $D\left(2010\right)=13562$ and $D\left(2008\right)=10025$.

$\text{Average}\text{rate}\text{of}\text{change}=\frac{13562-10025}{2010-2008}$,

$=\frac{3537}{2}$,

$=1768.5$.

Therefore, the average rate of change of the debt from $2008-2010$ is $\$1768.5$ billion per year.

To determine

To calculate: The average rate of change of the debt fromyear $2011-2013$.

Answer to Problem 78AYU

Solution:

The average rate of change of the debt from $2011-2013$ is $\$974$ billion per year.

Explanation of Solution

Given Information:

The following data represents the U.S debt for the years $2007-2017$, and the debt is a function $D\left(y\right)$ for each year $y$:

$\begin{array}{cc}& \text{Debt}\\ \text{Year}& \left(\text{billions}\text{of}\text{dollars}\right)\\ 2007& 9008\\ 2008& 10,025\\ 2009& 11,910\\ 2010& 13,562\\ 2011& 14,790\\ 2012& 16,066\\ 2013& 16,738\\ 2014& 17,824\\ 2015& 18,151\\ 2016& 19,573\\ 2017& 20,245\end{array}$

Formula used:

The average rate of change of function $y=f\left(x\right)$ from $a$ to $b$ is defined as:

Average rate of change $=\frac{\Delta y}{\Delta x}=\frac{f\left(b\right)-f\left(a\right)}{b-a}$ where $a$ and $b$, $a\ne b$, are in the domain of $f\left(x\right)$.

Calculation:

The average rate of change of the debt from $2011-2013$ is

Average rate of change $=\frac{\Delta y}{\Delta x}=\frac{D\left(2013\right)-D\left(2011\right)}{2013-2011}$.

From the table, $D\left(2013\right)=16738$ and $D\left(2011\right)=14790$.

Therefore, average rate of change $=\frac{16738-14790}{2013-2011}$

$=\frac{1948}{2}$

$=974$.

Therefore, the average rate of change of the debt from $2011-2013$ is $\$974$ billion per year.

To determine

To calculate: The average rate of change of the debt from $2014-2016$ year.

Answer to Problem 78AYU

Solution:

The average rate of change of the debt from $2014-2016$ is $\$874.5$ billion per year.

Explanation of Solution

Given Information:

The following data represents the U.S debt for the years $2007-2017$, and the debt is a function $D\left(y\right)$ for each year $y$:

$\begin{array}{cc}& \text{Debt}\\ \text{Year}& \left(\text{billions}\text{of}\text{dollars}\right)\\ 2007& 9008\\ 2008& 10,025\\ 2009& 11,910\\ 2010& 13,562\\ 2011& 14,790\\ 2012& 16,066\\ 2013& 16,738\\ 2014& 17,824\\ 2015& 18,151\\ 2016& 19,573\\ 2017& 20,245\end{array}$

Formula used:

The average rate of change of function $y=f\left(x\right)$ from $a$ to $b$ is defined as:

Average rate of change $=\frac{\Delta y}{\Delta x}=\frac{f\left(b\right)-f\left(a\right)}{b-a}$ where $a$ and $b$, $a\ne b$, are in the domain of $f\left(x\right)$.

Calculation:

The average rate of change of the debt from $2014-2016$ is

Average rate of change $=\frac{\Delta y}{\Delta x}=\frac{D\left(2016\right)-D\left(2014\right)}{2016-2014}$.

From the table, $D\left(2016\right)=19573$ and $D\left(2014\right)=17824$

Average rate of change $=\frac{19573-17824}{2016-2014}$

$=\frac{1749}{2}$

$=874.5$

Therefore, the average rate of change of the debt from $2014-2016$ is $\$874.5$ billion per year.

To determine

The effect on average rate of change as the time passes.

Answer to Problem 78AYU

Solution:

As time passes, the average rate of change of debt first increases and then decreases.

Explanation of Solution

Given Information:

The following data represents the U.S debt for the years $2007-2017$, and the debt is a function $D\left(y\right)$ for each year $y$:

$\begin{array}{cc}& \text{Debt}\\ \text{Year}& \left(\text{billions}\text{of}\text{dollars}\right)\\ 2007& 9008\\ 2008& 10,025\\ 2009& 11,910\\ 2010& 13,562\\ 2011& 14,790\\ 2012& 16,066\\ 2013& 16,738\\ 2014& 17,824\\ 2015& 18,151\\ 2016& 19,573\\ 2017& 20,245\end{array}$

Explanation:

The average rate of change of function $y=f\left(x\right)$ from $a$ to $b$ is defined as:

Average rate of change $=\frac{\Delta y}{\Delta x}=\frac{f\left(b\right)-f\left(a\right)}{b-a}$ where $a$ and $b$, $a\ne b$, are in the domain of $f\left(x\right)$.

From part (b), the slope of line segment from $2007-2012$ is $\$1411.6$ billion per year.

From part (c), the average rate of change of the debt from $2008-2010$ is $\$1768.5$ billion per year.

From part (d), the average rate of change of the debt from $2011-2013$ is $\$974$ billion per year.

From part (e), the average rate of change of the debt from $2014-2016$ is $\$874.5$ billion per year.

This shows that as time passes, the average rate of change of debt first increases and then decreases.