Chapter 2.6, Problem 25AYU

(a)

To determine

To express: the volume $V$ of the box as a function of the length $x$ of the side of the square cut from given corner

Answer to Problem 25AYU

The volume $V\left(x\right)=x{\left(24-2x\right)}^2$ .

Explanation of Solution

Given information:

A open box with a square base is to be made from a square piece of cardboard 24 inches on a side by cutting out a square from given corner and turning up the sides.

  

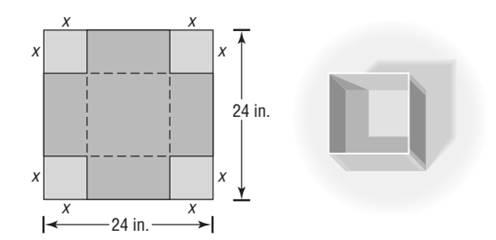
Calculation:

From the figure given in question, the following are the dimension of the open box made.

  $\begin{array}{c}\text{breadth}=\text{width}=24-2x\\ \text{height}=x\\ \text{Volume}\text{of}\text{the}\text{box}V=\text{breadth}\times \text{width}\times \text{height}\end{array}$

The volume as function of $x$ is

  $\begin{array}{c}V\left(x\right)=\left(24-2x\right)\left(24-2x\right)x\\ =x{\left(24-2x\right)}^2\end{array}$

(b)

To determine

To find: the volume if a 3 inch square is cut out.

Answer to Problem 25AYU

The volume $972{\text{in}}^{\text{3}}$ .

Explanation of Solution

Given information:

A open box with a square base is to be made from a square piece of cardboard 24 inches on a side by cutting out a square from given corner and turning up the sides.

  

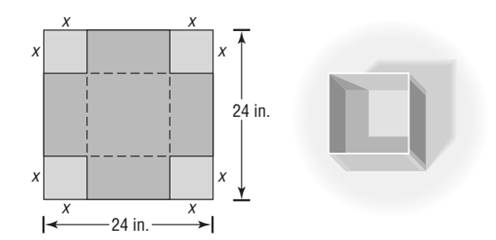
Calculation:

From part (a) at $x=3$ .

  $\begin{array}{c}V\left(3\right)=3{\left(24-2\times 3\right)}^2\\ =3{\left(18\right)}^2\\ =972{\text{in}}^{\text{3}}\end{array}$

(c)

To determine

To find: the volume if a10 inch square is cut out.

Answer to Problem 25AYU

The volume $160{\text{in}}^{\text{3}}$ .

Explanation of Solution

Given information:

A open box with a square base is to be made from a square piece of cardboard 24 inches on a side by cutting out a square from given corner and turning up the sides.

  

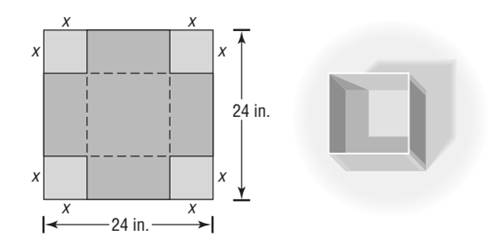
Calculation:

From part (a) at $x=10$ .

  $\begin{array}{c}V\left(10\right)=10{\left(24-2\times 10\right)}^2\\ =10{\left(4\right)}^2\\ =160{\text{in}}^{\text{3}}\end{array}$

(d)

To determine

To sketch: the graph of $V=V\left(x\right)$ , and to find the value of $x$ is $V$ largest.

Answer to Problem 25AYU

  $V\left(x\right)$ is largest when $x=4$ in.

Explanation of Solution

Given information:

A open box with a square base is to be made from a square piece of cardboard 24 inches on a side by cutting out a square from given corner and turning up the sides.

  

Calculation:

The graph of $V\left(x\right)=x{\left(24-2x\right)}^2$ is plotted below using Maple:

  

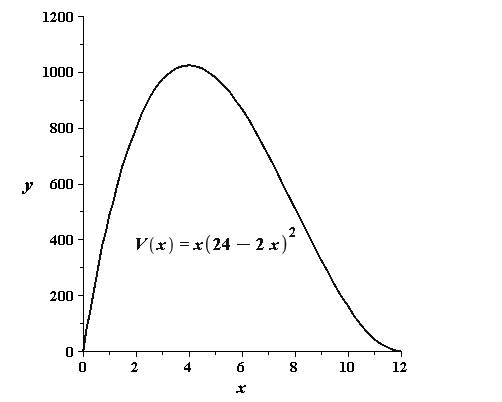
From the graph $V\left(x\right)$ is largest when $x=4$ in.