
Concept explainers
Use the given graph the function to answer parts (a)-(n).

(a) Find and .
(b) Find and .
(c) Is positive or negative?
(d) Is positive or negative?
(e) For what values of is ?
(f) For what values of is ?
(g) What is the domain of ?
(h) What is the range of ?
(i) What are the ?
(j) What is the ?
(k) How often does the line intersect the graph?
(l) How often does the line intersect the graph?
(m) For what values of does ?
(n) For what values of does ?
To find:
a. and .
Answer to Problem 9AYU
Solution:
a. ;
Explanation of Solution
Given:
The following graph
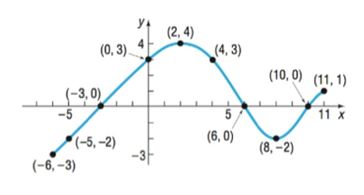
Calculation:
a. ;
To find:
b. and .
Answer to Problem 9AYU
Solution:
b. ;
Explanation of Solution
Given:
The following graph

Calculation:
b. ;
To find:
c. positive or negative.
Answer to Problem 9AYU
Solution:
c. is positive as the curve is above the ;
Explanation of Solution
Given:
The following graph

Calculation:
c. is positive as the curve is above the ;
To find:
d. positive or negative.
Answer to Problem 9AYU
Solution:
d. is negative as the curve is below the ;
Explanation of Solution
Given:
The following graph

Calculation:
d. is negative as the curve is below the ;
To find:
e. Value of for which .
Answer to Problem 9AYU
Solution:
e. when ;
Explanation of Solution
Given:
The following graph

Calculation:
e. when ;
To find:
f. Value of for which .
Answer to Problem 9AYU
Solution:
f. when ;
Explanation of Solution
Given:
The following graph

Calculation:
f. when ;
To find:
g. Domain of .
Answer to Problem 9AYU
Solution:
g. Domain of ;
Explanation of Solution
Given:
The following graph

Calculation:
g. Domain of ;
To find:
h. Range of .
Answer to Problem 9AYU
Solution:
h. Range of ;
Explanation of Solution
Given:
The following graph

Calculation:
h. Range of ;
To find:
i. Intercepts of .
Answer to Problem 9AYU
Solution:
i. Intercepts of ;
Explanation of Solution
Given:
The following graph

Calculation:
i. Intercepts of ;
To find:
j. Intercepts of .
Answer to Problem 9AYU
Solution:
j. Intercept of ;
Explanation of Solution
Given:
The following graph

Calculation:
j. Intercept of ;
To find:
k. Number of times the line intersect the graph.
Answer to Problem 9AYU
Solution:
k. The line crosses the curve three times;
Explanation of Solution
Given:
The following graph

Calculation:
k. The line crosses the curve three times;
To find:
l. Number of times the line intersect the graph.
Answer to Problem 9AYU
Solution:
l. The line crosses the curve only once;
Explanation of Solution
Given:
The following graph

Calculation:
l. The line crosses the curve only once;
To find:
m. The values of for which .
Answer to Problem 9AYU
Solution:
m. When ;
Explanation of Solution
Given:
The following graph

Calculation:
m. When ;
To find:
n. The values of for which .
Answer to Problem 9AYU
Solution:
n. When ;
Explanation of Solution
Given:
The following graph

Calculation:
n. When ;
Chapter 2 Solutions
Precalculus
Additional Math Textbook Solutions
University Calculus: Early Transcendentals (4th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Elementary Statistics
Elementary Statistics: Picturing the World (7th Edition)
Introductory Statistics
College Algebra (7th Edition)
- Force with 800 N and 400 N are acting on a machine part at 30° and 60°, respectively with the positive x axisarrow_forwardFind the accumulated amount A, if the principal P is invested at an interest rate of r per year for t years. (Round your answer to the nearest cent.) P = $13,000, r = 6%, t = 10, compounded quarterly A = $ 31902 Need Help? Read It Watch It Viewing Saved Work Revert to Last Response SUBMIT ANSWER O/6.66 Points] DETAILS MY NOTES TANAPCALC10 5.3.003. EVIOUS ANSWERS ASK YOUR TEACHER PRACTICE ANOTHER Find the accumulated amount A, if the principal P is invested at an interest rate of r per year for t years. (Round your answer to the nearest cent.) P = $140,000, r = 8%, t = 8, compounded monthly A = $259130.20 X Need Help? Read It Watch Itarrow_forwardFind the present value of $20,000 due in 3 years at the given rate of interest. (Round your answers to the nearest cent.) (a) 2%/year compounded monthly (b) 5%/year compounded daily $ Need Help? Read It Watch It SUBMIT ANSWER [-/6.66 Points] DETAILS MY NOTES TANAPCALC10 5.3.009. ASK YOUR TEACHER PRACTICE ANC Find the accumulated amount after 3 years if $4000 is invested at 3%/year compounded continuously. (Round your answer to the nearest cent.) Need Help? Read It Watch Itarrow_forward
- Find the effective rate corresponding to the given nominal rate. (Round your answers to three decimal places.) (a) 9.5%/year compounded monthly % (b) 9.5%/year compounded daily % Need Help? Read It Watch It SUBMIT ANSWER -/6.66 Points] DETAILS MY NOTES TANAPCALC10 5.3.007. ASK YOUR TEACHE Find the present value of $90,000 due in 7 years at the given rate of interest. (Round your answers to the nearest cent.) (a) 9%/year compounded semiannually (b) 9%/year compounded quarterly LAarrow_forwardFind the accumulated amount A, if the principal P is invested at an interest rate of r per year for t years. (Round your answer to the nearest cent.) P = $160,000, r = 7%, t = 4, compounded daily A = $211113.60 Need Help? Read It SUBMIT ANSWER ASK YOUR TEACHER PRACTICE ANOTHER --/6.66 Points] DETAILS MY NOTES TANAPCALC10 5.3.005. Find the effective rate corresponding to the given nominal rate. (Round your answers to three decimal places.) (a) 8%/year compounded semiannually % (b) 9%/year compounded quarterly %arrow_forwardFind the derivative of the function. g'(t) = 9t g(t) = In(t) (9ln(t) - 1) [In(t)] 2 × Need Help? Read It Watch Itarrow_forward
- Find the accumulated amount A, if the principal P is invested at an interest rate of r per year for t years. (Round your answer to the nearest cent.) P = $3800, r = 4%, t = 10, compounded semiannually A = $ 5645.60 × Need Help? Read It SUBMIT ANSWER [3.33/6.66 Points] DETAILS MY NOTES REVIOUS ANSWERS ASK YOUR TEACHER TANAPCALC10 5.3.001.EP. PRACTICE ANOTHER Consider the following where the principal P is invested at an interest rate of r per year for t years. P = $3,100, r = 4%, t = 10, compounded semiannually Determine m, the number of conversion periods per year. 2 Find the accumulated amount A (in dollars). (Round your answer to the nearest cent.) A = $ 4604.44arrow_forwardForce with 800 N and 400 N are acting on a machine part at 30° and 60°, respectively with a positive x axis, Draw the diagram representing this situationarrow_forwardI forgot to mention to you to solve question 1 and 2. Can you solve it using all data that given in the pict i given and can you teach me about that.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





