Chapter 2.2, Problem 44AYU

(a)

To determine

To find: the interval of time was M traveling fastest.

Answer to Problem 44AYU

The maximum value of $v\left(t\right)$ occurs between $t=7$ minutes and 1y $t=7.4$ minutes.

Explanation of Solution

Given information:

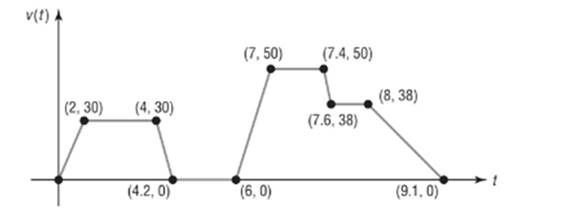
The following sketch represents the speed $v$ of M’s car as a function of time $t$

  

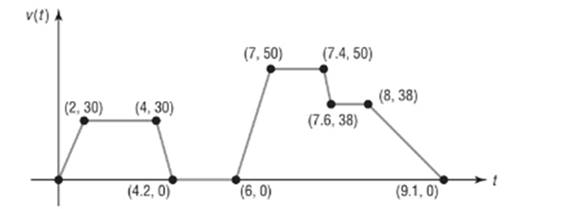
Calculation:

From the graph, the maximum value of $v\left(t\right)$ occurs between $t=7$ minutes and $t=7.4$ minutes.

(b)

To determine

To find: the interval of time was M’s speed zero.

Answer to Problem 44AYU

The maximum value of $v\left(t\right)$ occurs between $t=7$ minutes and $t=7.4$ minutes.

Explanation of Solution

Given information:

The following sketch represents the speed $v$ of M’s car as a function of time $t$

  

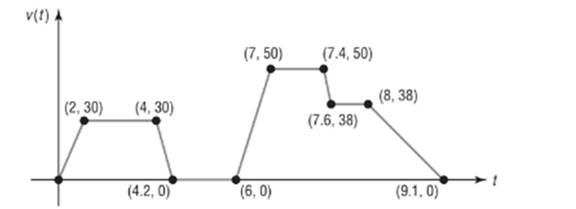
Calculation:

From the graph, the maximum value of $v\left(t\right)$ occurs between $t=7$ minutes and $t=7.4$ minutes.

(c)

To determine

To find: the M’s speed between 0 and 2 minutes

Answer to Problem 44AYU

We can represent the function $v\left(t\right)$ as

  $v\left(t\right)=15t,0\le t\le 2$

Explanation of Solution

Given information:

The following sketch represents the speed $v$ of M’s car as a function of time $t$

  

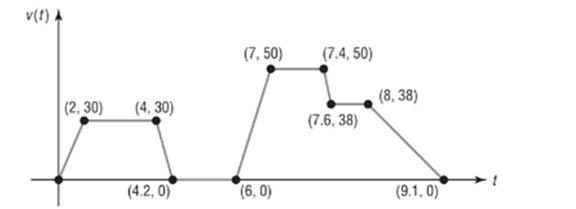
Calculation:

Between $t=0$ and $t=2$ , the speed increases linearly with timw. We can represent the function $v\left(t\right)$ as

  $\begin{array}{c}v\left(t\right)=\frac{30}{2}t\\ =15t,0\le t\le 2\end{array}$

(d)

To determine

To find: the M’s speed between 4.2 and 6 minutes

Answer to Problem 44AYU

The graph, the value of $v\left(t\right)$ is 0 between $t=4.2$ minutes and $t=6$ minutes.

Explanation of Solution

Given information:

The following sketch represents the speed $v$ of M’s car as a function of time $t$

  

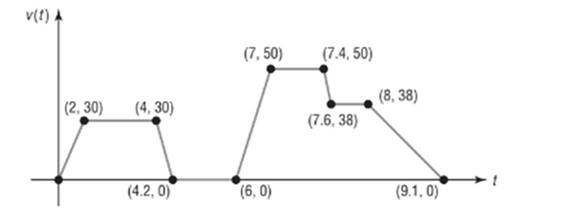
Calculation:

From the graph, the value of $v\left(t\right)$ is 0 between $t=4.2$ minutes and $t=6$ minutes.

(e)

To determine

To find: the M’s speed between 7 and 7.4 minutes

Answer to Problem 44AYU

The graph, the value of $v\left(t\right)$ is 50 miles per hour between $t=7$ minutes and $t=7.4$ minutes.

Explanation of Solution

Given information:

The following sketch represents the speed $v$ of M’s car as a function of time $t$

  

Calculation:

From the graph, the value of $v\left(t\right)$ is 50 miles per hour between $t=7$ minutes and $t=7.4$ minutes.

(f)

To determine

To find: When M’s speed constant.

Answer to Problem 44AYU

  $\begin{array}{l}\left(\text{2,4}\right)\left\{\text{speed}\text{is}\text{30}\text{miles}\text{per}\text{hour}\right\}\\ \left(\text{4,2,6}\right)\left\{\text{speed}\text{is}\text{0}\text{miles}\text{per}\text{hour}\right\}\\ \left(\text{7,7,4}\right)\left\{\text{speed}\text{is}\text{50}\text{miles}\text{per}\text{hour}\right\}\\ \left(\text{7,6,8}\right)\left\{\text{speed}\text{is}\text{38}\text{miles}\text{per}\text{hour}\right\}\end{array}$

Explanation of Solution

Given information:

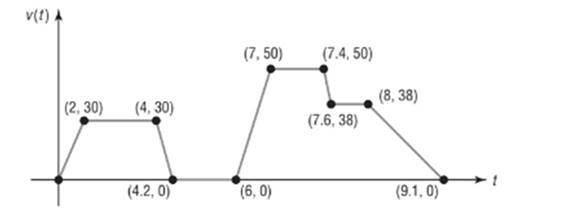
The following sketch represents the speed $v$ of M’s car as a function of time $t$

  

Calculation:

M’s speed is constant between the following time intervals.

  $\begin{array}{l}\left(\text{2,4}\right)\left\{\text{speed}\text{is}\text{30}\text{miles}\text{per}\text{hour}\right\}\\ \left(\text{4,2,6}\right)\left\{\text{speed}\text{is}\text{0}\text{miles}\text{per}\text{hour}\right\}\\ \left(\text{7,7,4}\right)\left\{\text{speed}\text{is}\text{50}\text{miles}\text{per}\text{hour}\right\}\\ \left(\text{7,6,8}\right)\left\{\text{speed}\text{is}\text{38}\text{miles}\text{per}\text{hour}\right\}\end{array}$