Chapter 2.3, Problem 60AYU

In Problems 57-64, use a graphing utility to graph each function over the indicated interval and approximate any local maximum values and local minimum values. Determine where the function is increasing and where it is decreasing. Round answers to two decimal places.

64. $f\left(x\right)=-0.4x^4-0.5x^3+0.8x^2-2\left[-3,2\right]$

To determine

To find: The following values using the given graph,

a. Draw the graph using graphing utility and determine the local maximum and minimum values.

Answer to Problem 60AYU

a. Local maximum point are $(-1.57,0.52)$ and $(0.64,-1.87)$ and local minimum is $(0,-2)$.

Explanation of Solution

Given:

It is asked to draw the graph using graphing utility and determine the local maximum and minimum values and also the increasing and decreasing intervals of the given function.

Calculation:

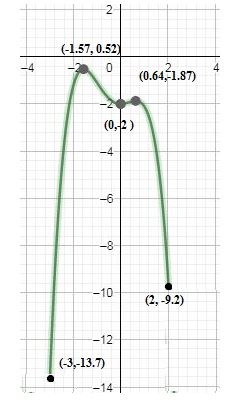
a. By the definition of local maximum, “Let $f$ be a function defined on some interval $I$. A function $f$ has a local maximum at $c$ if there is an open interval $I$ containing $c$ so that, for all $x$ in this open interval, we have $f\left(x\right)\le f\left(c\right)$. We call $f\left(c\right)$ a local maximum value of $f$”, It can be directly concluded from the graph and the definition that the curve has local maximum point at $x=-1.57$ and $x=0.64$.

The value of the local maximum at $x=-1.57$ is $0.52$ and $x=0.64$ is $-1.87$.

Therefore, the local maximum points are $(-1.57,0.52)$ and $(0.64,-1.87)$.

By the definition of local minimum, “Let $f$ be a function defined on some interval $I$. A function $f$ has a local minimum at $c$ if there is an open interval $I$ containing $c$ so that, for all $x$ in this open interval, we have $f\left(x\right)\ge f\left(c\right)$. We call $f\left(c\right)$ a local minimum value of $f$”, It can be directly concluded from the graph and the definition that the curve has local minimum point at $x=0$.

The value of the local minimum point at $x=0$ is $-2$.

Therefore, the local minimum point is $(0, -2)$.

To determine

To find: The following values using the given graph,

b. Increasing and decreasing intervals of the function $f$.

Answer to Problem 60AYU

b. The function $f$ is increasing in the interval $\underset{}{\left[-3,-1.57\right]}$ and $\left[0,0.64\right]$, the function $f$ is decreasing in the intervals $\left[-1.57,0\right]$ and $\left[0.64,-9.2\right]$. There is no constant interval in the given graph.

Explanation of Solution

Given:

It is asked to draw the graph using graphing utility and determine the local maximum and minimum values and also the increasing and decreasing intervals of the given function.

Calculation:

b. Increasing intervals, decreasing intervals and constant interval if any.

It can be directly concluded from the graph that the curve is increasing from $-3$ to $-1.57$, then decreasing from $-1.57$ to 0, then increasing from 0 to $0.64$ and at last decreasing from $0.64$ to 2.

Therefore, the function $f$ is increasing in the interval $\left[-3, -1.57\right]$ and $\left[0, 0.64\right]$, the function $f$ is decreasing in the intervals $\left[-1.57,0\right]$ and $\left[0.64,-9.2\right]$. There is no constant interval in the given graph.