Chapter 2.4, Problem 32AYU

(a)

To determine

To find: the domain of the given function.

Answer to Problem 32AYU

The function is not defined.

Explanation of Solution

Given information:

Given function

  $f\left(x\right)=\{\begin{array}{l}x+3\text{if}x<-2\\ -2x-3\text{if}x\ge -2\end{array}$

Calculation:

From the above definition we see the domain of the function is the set of all real numbers as there is no value of $x$ where the function is not defined.

(b)

To determine

To locate: any intercepts of the given function.

Answer to Problem 32AYU

  $x$ intercept at $\left(-3,0\right),\left(-\frac{3}{2},0\right)$ .

And the $y$ intercept is $\left(0,-3\right)$ .

Explanation of Solution

Given information:

Given function

  $f\left(x\right)=\{\begin{array}{l}x+3\text{if}x<-2\\ -2x-3\text{if}x\ge -2\end{array}$

Calculation:

The intercepts are the points on the graph which are obtained when it cuts the $x$ and $y$ axes. The point $\left(-3,0\right),\left(-\frac{3}{2},0\right)$ and $\left(0,-3\right)$ satisfy the function above. Hence the function has a $x$ intercept at $\left(-3,0\right),\left(-\frac{3}{2},0\right)$ .

And the $y$ intercept is $\left(0,-3\right)$ .

(c)

To determine

To sketch: the graph of the given function.

Explanation of Solution

Given information:

Given function

  $f\left(x\right)=\{\begin{array}{l}x+3\text{if}x<-2\\ -2x-3\text{if}x\ge -2\end{array}$

Calculation:

Plot the points and draw the line to get the graph of the function

  

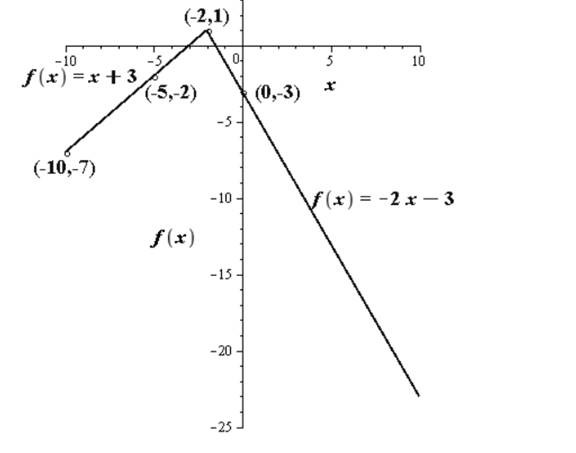
(d)

To determine

To find: the range based on the graph.

Answer to Problem 32AYU

The function $f\left(x\right)$ is the set $\left\{y|y\le 1\right\}$ .

Explanation of Solution

Given information:

Given function

  $f\left(x\right)=\{\begin{array}{l}x+3\text{if}x<-2\\ -2x-3\text{if}x\ge -2\end{array}$

Calculation:

From the graph we see that $f\left(x\right)\le 1$ in its domain. So the range of the function $f\left(x\right)$ is the set $\left\{y|y\le 1\right\}$ .

(e)

To determine

To find: whether $f$ continuous on its domain or not.

Answer to Problem 32AYU

The graph it can be clearly seen that the function is continuous throughout its domain.

Explanation of Solution

Given information:

Given function

  $f\left(x\right)=\{\begin{array}{l}x+3\text{if}x<-2\\ -2x-3\text{if}x\ge -2\end{array}$

Calculation:

The only point at which the function might have behaved in a manner that it becomes discontinuous is $x=-2$ . But at this point, the value of the function from the left of $-2$ and the right of $-2$ are given as:

  $\begin{array}{c}f\left(2^{-}\right)=-2+3\\ =1\end{array}$

and

  $\begin{array}{c}f\left(2^{+}\right)=-2\left(-2\right)+3\\ =4-3\\ =1\end{array}$

Hence $f\left(2^{+}\right)=f\left(2^{-}\right)$

So even at the break point the function is continous.

Hence the function is continuous at all points.

Also from the graph it can be clearly seen that the function is continuous throughout its domain.