Chapter 2.4, Problem 36AYU

(a)

To determine

To find: the domain of the given function.

Answer to Problem 36AYU

The domain of the function is the set of all real numbers.

Explanation of Solution

Given information:

Given function

  $f\left(x\right)=\{\begin{array}{l}\frac{1}{x}\text{\hspace{1em}if}x<0\\ \sqrt[3]{x}\text{\hspace{1em}if}x\ge 0\end{array}$

Calculation:

From the above definition we see the domain of the function is the set of all real numbers.

(b)

To determine

To locate: any intercepts of the given function.

Answer to Problem 36AYU

The function has a $x$ and $y$ intercept at $\left(0,0\right)$ .

Explanation of Solution

Given information:

Given function

  $f\left(x\right)=\{\begin{array}{l}\frac{1}{x}\text{\hspace{1em}if}x<0\\ \sqrt[3]{x}\text{\hspace{1em}if}x\ge 0\end{array}$

Calculation:

The intercepts are the points on the graph which are obtained when it cuts the $x$ and $y$ axes. The points $\left(0,0\right)$ satisfy the function above. Hence the function has a $x$ and $y$ intercept at $\left(0,0\right)$ .

(c)

To determine

To sketch: the graph of the given function.

Explanation of Solution

Given information:

Given function

  $f\left(x\right)=\{\begin{array}{l}\frac{1}{x}\text{\hspace{1em}if}x<0\\ \sqrt[3]{x}\text{\hspace{1em}if}x\ge 0\end{array}$

Calculation:

Plot the points and draw the line to get the graph of the function

  

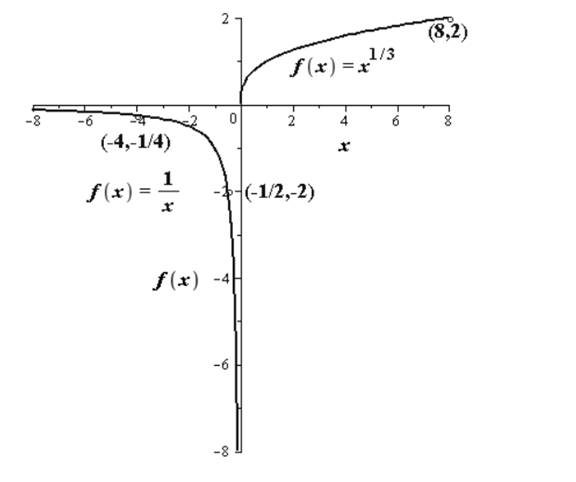
(d)

To determine

To find: the range based on the graph.

Answer to Problem 36AYU

The range of the function $f\left(x\right)$ is the set of real numbers.

Explanation of Solution

Given information:

Given function

  $f\left(x\right)=\{\begin{array}{l}\frac{1}{x}\text{\hspace{1em}if}x<0\\ \sqrt[3]{x}\text{\hspace{1em}if}x\ge 0\end{array}$

Calculation:

From the graph we see that $f\left(x\right)$ achieves all the real values in its domain. So the range of the function $f\left(x\right)$ is the set of real numbers.

(e)

To determine

To find: whether $f$ continuous on its domain or not.

Answer to Problem 36AYU

The graph it can be clearly seen that the function is discontinuous at the point $x=0$ .

Explanation of Solution

Given information:

Given function

  $f\left(x\right)=\{\begin{array}{l}\frac{1}{x}\text{\hspace{1em}if}x<0\\ \sqrt[3]{x}\text{\hspace{1em}if}x\ge 0\end{array}$

Calculation:

The only point at which the function might have behaved in a manner that it becomes discontinuous is $x=0$ . But at this point, the value of the function from the left of 0 and the right of 0 are given as:

  $\begin{array}{c}f\left(0^{-}\right)=\frac{1}{-0}\\ =-\infty \end{array}$

And

  $\begin{array}{c}f\left(0\right)=\sqrt[3]{0}\\ =0\end{array}$

And

  $\begin{array}{c}f\left(0^{+}\right)=\sqrt[3]{0}\\ =0\end{array}$

Hence

  $\begin{array}{c}f\left(0^{+}\right)\ne f\left(0\right)\\ \ne f\left(0^{-}\right)\end{array}$

So even at the break point the function is discontinuous.

Hence the function is discontinuous in its domain only at the point $x=0$ .

Also from the graph it can be clearly seen that the function is discontinuous at the point $x=0$ .