a)

To plot: A box plot for the set of data where the median is less than the mean of the data distribution.

The set of data where the median is less than the mean and its box plot are shown below

1, 2, 3, 3, 4, 4, 5, 5, 6, 6, 6, 7, 7, 10, 15.

Given:

The collected set of data is 1, 2, 3, 3, 4, 4, 5, 5, 6, 6, 6, 7, 7, 10, 15.

Concept used:

The mean and median are measures of central tendency, the mean is nothing but the average of all values and the median is the middle value of the data distribution in ascending order.

The mean is calculated using the formula

Mean=∑Xn

The box plot consists of a box and whisker where it shows five number summary (minimum, first quartile, median, third quartile, maximum). The first quartile divides the data distribution bottom 25% and the top 75% of the data and quartile three divides the bottom 75% and the top 25% of the data.

Calculation:

The mean of the set of data is calculated as shown below

Mean=∑Xn=1+2+3+3+4+4+5+5+6+6+6+7+7+10+1515=8415=5.6

There are a total of 15 data points given in the data distribution arranging them in ascending order, the median of the data distribution is the middle value which is at the 8^t^h position.

With reference to the given set of data values, the data point at the 8^t^h position is 5. The mean of the data distribution is 5.6 and the median is 5.

Thus for the given data median is less than the mean. The first quartile divides the bottom 25% of the data and the top 75% of the data, it is nothing but the middle value of the values of the first half of the data i.e.

1, 2, 3, 3, 4, 4, 5, 5. There are a total of 8 data values and the middle value is the average of data values at 4^t^h and 5^t^h positions.

Q1First Quartile=3+42=3.5

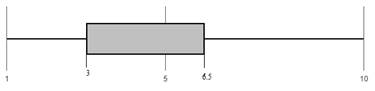
The first quartile is 3.5.

The third quartile divides the bottom 75% of the data and the top 25% of the data, it is nothing but the middle value of the values of the second half of the data i.e.

5, 6, 6, 6, 7, 7, 10, 15. There are a total of 8 data values and the middle value is the average of data values at 4^t^h and 5^t^h positions.

Q3Third Quartile=6+72=6.5

The third quartile is 6.5.

The minimum and maximum values of the set of data are 1 and 15 respectively. Thus the five-number summary of the given data set is 1, 3.5, 5, 6.5, 15

Plot:With reference to the five number summary the box plot is sketched as shown below

b)

To plot: A box plot for set of data where twice the interquartile range is less than the range of the data distribution.

The set of data where twice the interquartile range is less than the range and its box plot is shown below

1, 2, 3, 3, 4, 4, 5, 5, 6, 6, 6, 7, 7, 10, 15.

Given:

The collected set of data is 1, 2, 3, 3, 4, 4, 5, 5, 6, 6, 6, 7, 7, 10, 15.

Concept used:

The interquartile range are measures of variability, and it is the range of the middle 50% values of the data distribution. The Interquartile range is the difference between the third Quartile and the first Quartile, where the first quartile divides the data distribution bottom 25% and top 75% of the data and the quartile three divides the data bottom 75% and top 25% of the data.The range is the difference between the maximum and minimum value of the data distribution.

Calculation:

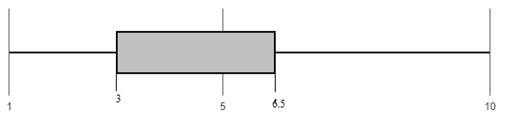
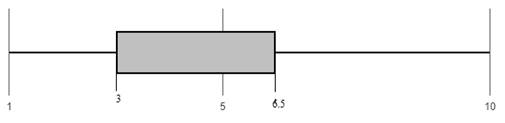
The first quartile is 3.5 and the third quartile is 6.5. The median of the data distribution is 5.

The minimum value of the data distribution is 1 and the maximum value of the data distribution is 15.

The Interquartile range of the set of data is the difference between the third quartile and first quartile and is calculated as shown below

IQR=Q3−Q1=6.5−3.5=3

The range of the data distribution is calculated as shown below

Range=Maximum−Minimum=15−1=14

The value of twice the Interquartile range is =2×IQR=2×3=6

Thus the given condition twice the interquartile range (6) is less than range (14) is satisfied.

Plot:With reference to the five number summary 1, 3.5, 5, 6.5, 15 the box plot is sketched as shown below

c)

To plot: A box plot for the set of data where the range is less than twice the interquartile range of the data distribution.

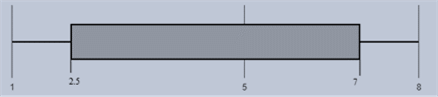
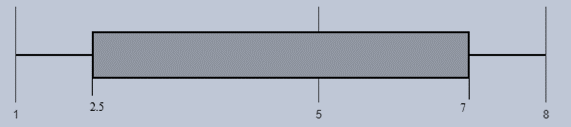
The set of data where the range is less than twice the interquartile range and its box plot is shown below

1, 2, 2, 2, 3, 4, 5, 5, 6, 6, 7, 7, 7, 7, 8.

Given:

The collected set of data is 1, 2, 2, 2, 3, 4, 5, 5, 6, 6, 7, 7, 7, 7, 8.

Calculation:

There are a total of 15 data points given in the data distribution arranging them in ascending order, the median of the data distribution is the middle value which is at the 8^t^h position.

With reference to the given set of data values, the data point at the 8^t^h position is 5. The median is 5. The first quartile divides the bottom 25% of the data and the top 75% of the data, it is nothing but the middle value of the values of the first half of the data i.e.

1, 2, 2, 2, 3, 4, 5, 5. There are a total of 8 data values and the middle value is the average of data values at 4^t^h and 5^t^h positions.

Q1First Quartile=2+32=2.5

The first quartile is 2.5.

The third quartile divides the bottom 75% of the data and the top 25% of the data, it is nothing but the middle value of the values of the second half of the data i.e.

5, 6, 6, 7, 7, 7, 7, 8. There are a total of 8 data values and the middle value is the average of data values at 4^t^h and 5^t^h positions.

Q3Third Quartile=7+72=7

The third quartile is 7.

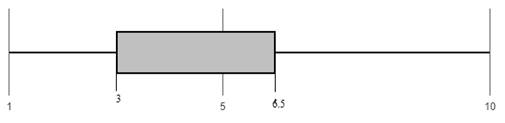
The minimum and maximum values of the set of data are 1 and 8 respectively. Thus the five-number summary of the given data set is 1, 2.5, 5, 7, 8 .

The Interquartile range of the set of data is the difference between the third quartile and first quartile and is calculated as shown below

IQR=Q3−Q1=7−2.5=5.5

The range of the data distribution is calculated as shown below

Range=Maximum−Minimum=8−1=7

The value of twice the Interquartile range is =2×IQR=2×5.5=11

Thus the given condition twice the interquartile range (11) is more than range (7) is satisfied

Plot:With reference to the five number summary 1, 2.5, 5, 7, 8 the box plot is sketched as shown below

Chapter 10.3, Problem 54E

Chapter 10.3, Problem 56E

Chapter 10 Solutions

PRECALCULUS:GRAPHICAL,...-NASTA ED.

Ch. 10.1 - Prob. 1QR Ch. 10.1 - Prob. 2QR Ch. 10.1 - Prob. 3QR Ch. 10.1 - Prob. 4QR Ch. 10.1 - Prob. 5QR Ch. 10.1 - Prob. 6QR Ch. 10.1 - Prob. 7QR Ch. 10.1 - Prob. 8QR Ch. 10.1 - Prob. 9QR Ch. 10.1 - Prob. 10QR

Ch. 10.1 - Prob. 1E Ch. 10.1 - Prob. 2E Ch. 10.1 - Prob. 3E Ch. 10.1 - Prob. 4E Ch. 10.1 - Prob. 5E Ch. 10.1 - Prob. 6E Ch. 10.1 - Prob. 7E Ch. 10.1 - Prob. 8E Ch. 10.1 - Prob. 9E Ch. 10.1 - Prob. 10E Ch. 10.1 - Prob. 11E Ch. 10.1 - Prob. 12E Ch. 10.1 - Prob. 13E Ch. 10.1 - Prob. 14E Ch. 10.1 - Prob. 15E Ch. 10.1 - Prob. 16E Ch. 10.1 - Prob. 17E Ch. 10.1 - Prob. 18E Ch. 10.1 - Prob. 19E Ch. 10.1 - Prob. 20E Ch. 10.1 - Prob. 21E Ch. 10.1 - Prob. 22E Ch. 10.1 - Prob. 23E Ch. 10.1 - Prob. 24E Ch. 10.1 - Prob. 25E Ch. 10.1 - Prob. 26E Ch. 10.1 - Prob. 27E Ch. 10.1 - Prob. 28E Ch. 10.1 - Prob. 29E Ch. 10.1 - Prob. 30E Ch. 10.1 - Prob. 31E Ch. 10.1 - Prob. 32E Ch. 10.1 - Prob. 33E Ch. 10.1 - Prob. 34E Ch. 10.1 - Prob. 35E Ch. 10.1 - Prob. 36E Ch. 10.1 - Prob. 37E Ch. 10.1 - Prob. 38E Ch. 10.1 - Prob. 39E Ch. 10.1 - Prob. 40E Ch. 10.1 - Prob. 41E Ch. 10.1 - Prob. 42E Ch. 10.1 - Prob. 43E Ch. 10.1 - Prob. 44E Ch. 10.1 - Prob. 45E Ch. 10.1 - Prob. 46E Ch. 10.1 - Prob. 47E Ch. 10.1 - Prob. 48E Ch. 10.1 - Prob. 49E Ch. 10.1 - Prob. 50E Ch. 10.1 - Prob. 51E Ch. 10.1 - Prob. 52E Ch. 10.1 - Prob. 53E Ch. 10.1 - Prob. 54E Ch. 10.1 - Prob. 55E Ch. 10.1 - Prob. 56E Ch. 10.1 - Prob. 57E Ch. 10.1 - Prob. 58E Ch. 10.1 - Prob. 59E Ch. 10.1 - Prob. 60E Ch. 10.1 - Prob. 61E Ch. 10.1 - Prob. 62E Ch. 10.2 - Prob. 1QR Ch. 10.2 - Prob. 2QR Ch. 10.2 - Prob. 3QR Ch. 10.2 - Prob. 4QR Ch. 10.2 - Prob. 5QR Ch. 10.2 - Prob. 6QR Ch. 10.2 - Prob. 7QR Ch. 10.2 - Prob. 8QR Ch. 10.2 - Prob. 9QR Ch. 10.2 - Prob. 10QR Ch. 10.2 - Prob. 1E Ch. 10.2 - Prob. 2E Ch. 10.2 - Prob. 3E Ch. 10.2 - Prob. 4E Ch. 10.2 - Prob. 5E Ch. 10.2 - Prob. 6E Ch. 10.2 - Prob. 7E Ch. 10.2 - Prob. 8E Ch. 10.2 - Prob. 9E Ch. 10.2 - Prob. 10E Ch. 10.2 - Prob. 11E Ch. 10.2 - Prob. 12E Ch. 10.2 - Prob. 13E Ch. 10.2 - Prob. 14E Ch. 10.2 - Prob. 15E Ch. 10.2 - Prob. 16E Ch. 10.2 - Prob. 17E Ch. 10.2 - Prob. 18E Ch. 10.2 - Prob. 19E Ch. 10.2 - Prob. 20E Ch. 10.2 - Prob. 21E Ch. 10.2 - Prob. 22E Ch. 10.2 - Prob. 23E Ch. 10.2 - Prob. 24E Ch. 10.2 - Prob. 25E Ch. 10.2 - Prob. 26E Ch. 10.2 - Prob. 27E Ch. 10.2 - Prob. 28E Ch. 10.2 - Prob. 29E Ch. 10.2 - Prob. 30E Ch. 10.2 - Prob. 31E Ch. 10.2 - Prob. 32E Ch. 10.2 - Prob. 33E Ch. 10.2 - Prob. 34E Ch. 10.2 - Prob. 35E Ch. 10.2 - Prob. 36E Ch. 10.2 - Prob. 37E Ch. 10.2 - Prob. 38E Ch. 10.2 - Prob. 39E Ch. 10.2 - Prob. 40E Ch. 10.2 - Prob. 41E Ch. 10.2 - Prob. 42E Ch. 10.2 - Prob. 43E Ch. 10.2 - Prob. 44E Ch. 10.2 - Prob. 45E Ch. 10.2 - Prob. 46E Ch. 10.2 - Prob. 47E Ch. 10.2 - Prob. 48E Ch. 10.3 - Prob. 1QR Ch. 10.3 - Prob. 2QR Ch. 10.3 - Prob. 3QR Ch. 10.3 - Prob. 4QR Ch. 10.3 - Prob. 5QR Ch. 10.3 - Prob. 6QR Ch. 10.3 - Prob. 7QR Ch. 10.3 - Prob. 8QR Ch. 10.3 - Prob. 9QR Ch. 10.3 - Prob. 10QR Ch. 10.3 - Prob. 1E Ch. 10.3 - Prob. 2E Ch. 10.3 - Prob. 3E Ch. 10.3 - Prob. 4E Ch. 10.3 - Prob. 5E Ch. 10.3 - Prob. 6E Ch. 10.3 - Prob. 7E Ch. 10.3 - Prob. 8E Ch. 10.3 - Prob. 9E Ch. 10.3 - Prob. 10E Ch. 10.3 - Prob. 11E Ch. 10.3 - Prob. 12E Ch. 10.3 - Prob. 13E Ch. 10.3 - Prob. 14E Ch. 10.3 - Prob. 15E Ch. 10.3 - Prob. 16E Ch. 10.3 - Prob. 17E Ch. 10.3 - Prob. 18E Ch. 10.3 - Prob. 19E Ch. 10.3 - Prob. 20E Ch. 10.3 - Prob. 21E Ch. 10.3 - Prob. 22E Ch. 10.3 - Prob. 23E Ch. 10.3 - Prob. 24E Ch. 10.3 - Prob. 25E Ch. 10.3 - Prob. 26E Ch. 10.3 - Prob. 27E Ch. 10.3 - Prob. 28E Ch. 10.3 - Prob. 29E Ch. 10.3 - Prob. 30E Ch. 10.3 - Prob. 31E Ch. 10.3 - Prob. 32E Ch. 10.3 - Prob. 33E Ch. 10.3 - Prob. 34E Ch. 10.3 - Prob. 35E Ch. 10.3 - Prob. 36E Ch. 10.3 - Prob. 37E Ch. 10.3 - Prob. 38E Ch. 10.3 - Prob. 39E Ch. 10.3 - Prob. 40E Ch. 10.3 - Prob. 41E Ch. 10.3 - Prob. 42E Ch. 10.3 - Prob. 43E Ch. 10.3 - Prob. 44E Ch. 10.3 - Prob. 45E Ch. 10.3 - Prob. 46E Ch. 10.3 - Prob. 47E Ch. 10.3 - Prob. 48E Ch. 10.3 - Prob. 49E Ch. 10.3 - Prob. 50E Ch. 10.3 - Prob. 51E Ch. 10.3 - Prob. 52E Ch. 10.3 - Prob. 53E Ch. 10.3 - Prob. 54E Ch. 10.3 - Prob. 55E Ch. 10.3 - Prob. 56E Ch. 10.3 - Prob. 57E Ch. 10.3 - Prob. 58E Ch. 10.3 - Prob. 59E Ch. 10.3 - Prob. 60E Ch. 10.4 - Prob. 1QR Ch. 10.4 - Prob. 2QR Ch. 10.4 - Prob. 3QR Ch. 10.4 - Prob. 4QR Ch. 10.4 - Prob. 5QR Ch. 10.4 - Prob. 6QR Ch. 10.4 - Prob. 7QR Ch. 10.4 - Prob. 8QR Ch. 10.4 - Prob. 9QR Ch. 10.4 - Prob. 10QR Ch. 10.4 - Prob. 1E Ch. 10.4 - Prob. 2E Ch. 10.4 - Prob. 3E Ch. 10.4 - Prob. 4E Ch. 10.4 - Prob. 5E Ch. 10.4 - Prob. 6E Ch. 10.4 - Prob. 7E Ch. 10.4 - Prob. 8E Ch. 10.4 - Prob. 9E Ch. 10.4 - Prob. 10E Ch. 10.4 - Prob. 11E Ch. 10.4 - Prob. 12E Ch. 10.4 - Prob. 13E Ch. 10.4 - Prob. 14E Ch. 10.4 - Prob. 15E Ch. 10.4 - Prob. 16E Ch. 10.4 - Prob. 17E Ch. 10.4 - Prob. 18E Ch. 10.4 - Prob. 19E Ch. 10.4 - Prob. 20E Ch. 10.4 - Prob. 21E Ch. 10.4 - Prob. 22E Ch. 10.4 - Prob. 23E Ch. 10.4 - Prob. 24E Ch. 10.4 - Prob. 25E Ch. 10.4 - Prob. 26E Ch. 10.4 - Prob. 27E Ch. 10.4 - Prob. 28E Ch. 10.4 - Prob. 29E Ch. 10.4 - Prob. 30E Ch. 10.4 - Prob. 31E Ch. 10.4 - Prob. 32E Ch. 10.4 - Prob. 33E Ch. 10.4 - Prob. 34E Ch. 10.4 - Prob. 35E Ch. 10.4 - Prob. 36E Ch. 10.4 - Prob. 37E Ch. 10.4 - Prob. 38E Ch. 10.4 - Prob. 39E Ch. 10.4 - Prob. 40E Ch. 10.4 - Prob. 41E Ch. 10.4 - Prob. 42E Ch. 10.4 - Prob. 43E Ch. 10.4 - Prob. 44E Ch. 10.4 - Prob. 45E Ch. 10.4 - Prob. 46E Ch. 10.4 - Prob. 47E Ch. 10.4 - Prob. 48E Ch. 10.4 - Prob. 49E Ch. 10.4 - Prob. 50E Ch. 10.4 - Prob. 51E Ch. 10.4 - Prob. 52E Ch. 10.4 - Prob. 53E Ch. 10.4 - Prob. 54E Ch. 10.4 - Prob. 55E Ch. 10.4 - Prob. 56E Ch. 10.5 - Prob. 1QR Ch. 10.5 - Prob. 2QR Ch. 10.5 - Prob. 3QR Ch. 10.5 - Prob. 4QR Ch. 10.5 - Prob. 5QR Ch. 10.5 - Prob. 6QR Ch. 10.5 - Prob. 7QR Ch. 10.5 - Prob. 8QR Ch. 10.5 - Prob. 9QR Ch. 10.5 - Prob. 10QR Ch. 10.5 - Prob. 1E Ch. 10.5 - Prob. 2E Ch. 10.5 - Prob. 3E Ch. 10.5 - Prob. 4E Ch. 10.5 - Prob. 5E Ch. 10.5 - Prob. 6E Ch. 10.5 - Prob. 7E Ch. 10.5 - Prob. 8E Ch. 10.5 - Prob. 9E Ch. 10.5 - Prob. 10E Ch. 10.5 - Prob. 11E Ch. 10.5 - Prob. 12E Ch. 10.5 - Prob. 13E Ch. 10.5 - Prob. 14E Ch. 10.5 - Prob. 15E Ch. 10.5 - Prob. 16E Ch. 10.5 - Prob. 17E Ch. 10.5 - Prob. 18E Ch. 10.5 - Prob. 19E Ch. 10.5 - Prob. 20E Ch. 10.5 - Prob. 21E Ch. 10.5 - Prob. 22E Ch. 10.5 - Prob. 23E Ch. 10.5 - Prob. 24E Ch. 10.5 - Prob. 25E Ch. 10.5 - Prob. 26E Ch. 10.5 - Prob. 27E Ch. 10.5 - Prob. 28E Ch. 10.5 - Prob. 29E Ch. 10.5 - Prob. 30E Ch. 10.5 - Prob. 31E Ch. 10.5 - Prob. 32E Ch. 10.5 - Prob. 33E Ch. 10.5 - Prob. 34E Ch. 10.5 - Prob. 35E Ch. 10.5 - Prob. 36E Ch. 10.5 - Prob. 37E Ch. 10.5 - Prob. 38E Ch. 10.5 - Prob. 39E Ch. 10.5 - Prob. 40E Ch. 10.5 - Prob. 41E Ch. 10.5 - Prob. 42E Ch. 10.5 - Prob. 43E Ch. 10.5 - Prob. 44E Ch. 10.5 - Prob. 45E Ch. 10.5 - Prob. 46E Ch. 10.5 - Prob. 47E Ch. 10.5 - Prob. 48E Ch. 10.5 - Prob. 49E Ch. 10.5 - Prob. 50E Ch. 10.5 - Prob. 51E Ch. 10.5 - Prob. 52E Ch. 10.5 - Prob. 55E Ch. 10.5 - Prob. 56E Ch. 10.5 - Prob. 59E Ch. 10.5 - Prob. 60E Ch. 10 - Prob. 1RE Ch. 10 - Prob. 2RE Ch. 10 - Prob. 3RE Ch. 10 - Prob. 4RE Ch. 10 - Prob. 5RE Ch. 10 - Prob. 6RE Ch. 10 - Prob. 7RE Ch. 10 - Prob. 8RE Ch. 10 - Prob. 9RE Ch. 10 - Prob. 10RE Ch. 10 - Prob. 11RE Ch. 10 - Prob. 12RE Ch. 10 - Prob. 13RE Ch. 10 - Prob. 14RE Ch. 10 - Prob. 15RE Ch. 10 - Prob. 16RE Ch. 10 - Prob. 17RE Ch. 10 - Prob. 18RE Ch. 10 - Prob. 19RE Ch. 10 - Prob. 20RE Ch. 10 - Prob. 21RE Ch. 10 - Prob. 22RE Ch. 10 - Prob. 23RE Ch. 10 - Prob. 24RE Ch. 10 - Prob. 25RE Ch. 10 - Prob. 26RE Ch. 10 - Prob. 27RE Ch. 10 - Prob. 28RE Ch. 10 - Prob. 29RE Ch. 10 - Prob. 30RE Ch. 10 - Prob. 31RE Ch. 10 - Prob. 32RE Ch. 10 - Prob. 33RE Ch. 10 - Prob. 34RE Ch. 10 - Prob. 35RE Ch. 10 - Prob. 36RE Ch. 10 - Prob. 37RE Ch. 10 - Prob. 38RE Ch. 10 - Prob. 39RE Ch. 10 - Prob. 40RE Ch. 10 - Prob. 41RE Ch. 10 - Prob. 42RE Ch. 10 - Prob. 43RE Ch. 10 - Prob. 44RE Ch. 10 - Prob. 45RE Ch. 10 - Prob. 46RE Ch. 10 - Prob. 47RE Ch. 10 - Prob. 48RE Ch. 10 - Prob. 49RE Ch. 10 - Prob. 50RE Ch. 10 - Prob. 51RE Ch. 10 - Prob. 52RE Ch. 10 - Prob. 53RE Ch. 10 - Prob. 54RE Ch. 10 - Prob. 55RE Ch. 10 - Prob. 56RE Ch. 10 - Prob. 57RE Ch. 10 - Prob. 58RE Ch. 10 - Prob. 59RE Ch. 10 - Prob. 60RE Ch. 10 - Prob. 61RE Ch. 10 - Prob. 62RE Ch. 10 - Prob. 63RE Ch. 10 - Prob. 64RE Ch. 10 - Prob. 65RE Ch. 10 - Prob. 66RE Ch. 10 - Prob. 67RE Ch. 10 - Prob. 68RE Ch. 10 - Prob. 69RE Ch. 10 - Prob. 70RE Ch. 10 - Prob. 71RE Ch. 10 - Prob. 72RE

Knowledge Booster

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning