PRECALCULUS:GRAPHICAL,...-NASTA ED.
10th Edition
ISBN: 9780134672090
Author: Demana
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Expert Solution & Answer
Chapter 10, Problem 24RE
Solution
To Create: The boxplot of the length of songs data and identify the outliers present in the data.
The boxplot is:
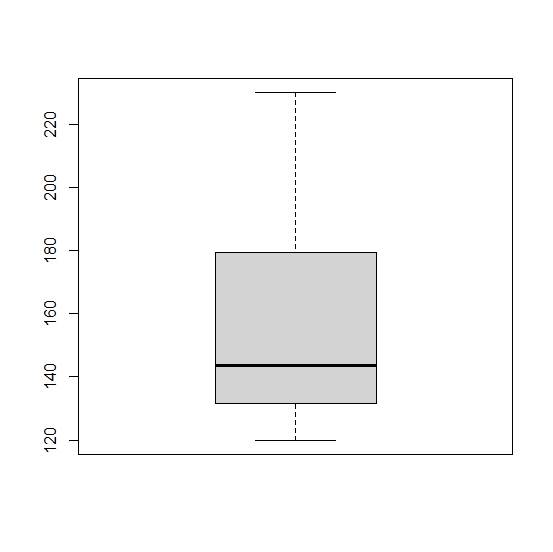
There are no outliers present in the data.
Given information:
The length (in seconds) of the songs is as follows:
| Length |
| 120 |
| 120 |
| 124 |
| 124 |
| 131 |
| 131 |
| 132 |
| 136 |
| 137 |
| 139 |
| 140 |
| 143 |
| 144 |
| 148 |
| 156 |
| 163 |
| 177 |
| 179 |
| 180 |
| 190 |
| 191 |
| 197 |
| 202 |
| 230 |
Concept Used:
The boxplot is created in the following steps:
Step 1: Arrange the data in ascending order.
Step 2: Compute the quartiles of the data as
Step 3: Consider the data on y-axis and plot the quartiles to obtain the box.
Step 4: Now compute the lower limit and upper limit to find the length of whiskers as follows,
Step 5: Plot the limits and connect the points with the box obtained using the quartiles.
Plot:
The boxplot created using the above steps is:
Here
The five-number summary is
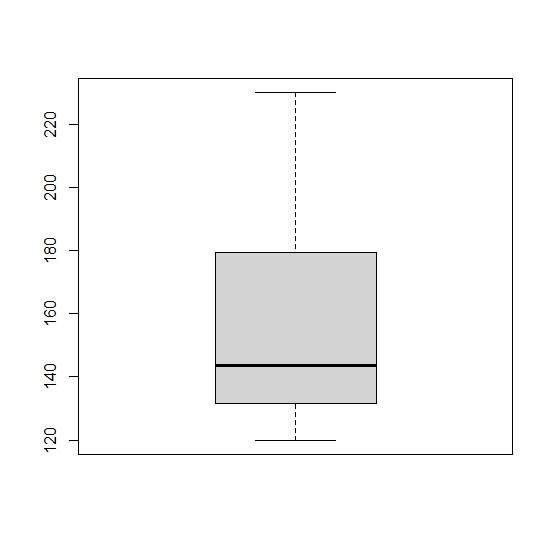
Outliers:
There are no data points lying outside the whiskers of the boxplot. So there are no outliers present in the length of the songs data.
Chapter 10 Solutions
PRECALCULUS:GRAPHICAL,...-NASTA ED.
Ch. 10.1 - Prob. 1QRCh. 10.1 - Prob. 2QRCh. 10.1 - Prob. 3QRCh. 10.1 - Prob. 4QRCh. 10.1 - Prob. 5QRCh. 10.1 - Prob. 6QRCh. 10.1 - Prob. 7QRCh. 10.1 - Prob. 8QRCh. 10.1 - Prob. 9QRCh. 10.1 - Prob. 10QR
Ch. 10.1 - Prob. 1ECh. 10.1 - Prob. 2ECh. 10.1 - Prob. 3ECh. 10.1 - Prob. 4ECh. 10.1 - Prob. 5ECh. 10.1 - Prob. 6ECh. 10.1 - Prob. 7ECh. 10.1 - Prob. 8ECh. 10.1 - Prob. 9ECh. 10.1 - Prob. 10ECh. 10.1 - Prob. 11ECh. 10.1 - Prob. 12ECh. 10.1 - Prob. 13ECh. 10.1 - Prob. 14ECh. 10.1 - Prob. 15ECh. 10.1 - Prob. 16ECh. 10.1 - Prob. 17ECh. 10.1 - Prob. 18ECh. 10.1 - Prob. 19ECh. 10.1 - Prob. 20ECh. 10.1 - Prob. 21ECh. 10.1 - Prob. 22ECh. 10.1 - Prob. 23ECh. 10.1 - Prob. 24ECh. 10.1 - Prob. 25ECh. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - Prob. 28ECh. 10.1 - Prob. 29ECh. 10.1 - Prob. 30ECh. 10.1 - Prob. 31ECh. 10.1 - Prob. 32ECh. 10.1 - Prob. 33ECh. 10.1 - Prob. 34ECh. 10.1 - Prob. 35ECh. 10.1 - Prob. 36ECh. 10.1 - Prob. 37ECh. 10.1 - Prob. 38ECh. 10.1 - Prob. 39ECh. 10.1 - Prob. 40ECh. 10.1 - Prob. 41ECh. 10.1 - Prob. 42ECh. 10.1 - Prob. 43ECh. 10.1 - Prob. 44ECh. 10.1 - Prob. 45ECh. 10.1 - Prob. 46ECh. 10.1 - Prob. 47ECh. 10.1 - Prob. 48ECh. 10.1 - Prob. 49ECh. 10.1 - Prob. 50ECh. 10.1 - Prob. 51ECh. 10.1 - Prob. 52ECh. 10.1 - Prob. 53ECh. 10.1 - Prob. 54ECh. 10.1 - Prob. 55ECh. 10.1 - Prob. 56ECh. 10.1 - Prob. 57ECh. 10.1 - Prob. 58ECh. 10.1 - Prob. 59ECh. 10.1 - Prob. 60ECh. 10.1 - Prob. 61ECh. 10.1 - Prob. 62ECh. 10.2 - Prob. 1QRCh. 10.2 - Prob. 2QRCh. 10.2 - Prob. 3QRCh. 10.2 - Prob. 4QRCh. 10.2 - Prob. 5QRCh. 10.2 - Prob. 6QRCh. 10.2 - Prob. 7QRCh. 10.2 - Prob. 8QRCh. 10.2 - Prob. 9QRCh. 10.2 - Prob. 10QRCh. 10.2 - Prob. 1ECh. 10.2 - Prob. 2ECh. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - Prob. 12ECh. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - Prob. 15ECh. 10.2 - Prob. 16ECh. 10.2 - Prob. 17ECh. 10.2 - Prob. 18ECh. 10.2 - Prob. 19ECh. 10.2 - Prob. 20ECh. 10.2 - Prob. 21ECh. 10.2 - Prob. 22ECh. 10.2 - Prob. 23ECh. 10.2 - Prob. 24ECh. 10.2 - Prob. 25ECh. 10.2 - Prob. 26ECh. 10.2 - Prob. 27ECh. 10.2 - Prob. 28ECh. 10.2 - Prob. 29ECh. 10.2 - Prob. 30ECh. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - Prob. 35ECh. 10.2 - Prob. 36ECh. 10.2 - Prob. 37ECh. 10.2 - Prob. 38ECh. 10.2 - Prob. 39ECh. 10.2 - Prob. 40ECh. 10.2 - Prob. 41ECh. 10.2 - Prob. 42ECh. 10.2 - Prob. 43ECh. 10.2 - Prob. 44ECh. 10.2 - Prob. 45ECh. 10.2 - Prob. 46ECh. 10.2 - Prob. 47ECh. 10.2 - Prob. 48ECh. 10.3 - Prob. 1QRCh. 10.3 - Prob. 2QRCh. 10.3 - Prob. 3QRCh. 10.3 - Prob. 4QRCh. 10.3 - Prob. 5QRCh. 10.3 - Prob. 6QRCh. 10.3 - Prob. 7QRCh. 10.3 - Prob. 8QRCh. 10.3 - Prob. 9QRCh. 10.3 - Prob. 10QRCh. 10.3 - Prob. 1ECh. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - Prob. 17ECh. 10.3 - Prob. 18ECh. 10.3 - Prob. 19ECh. 10.3 - Prob. 20ECh. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - Prob. 24ECh. 10.3 - Prob. 25ECh. 10.3 - Prob. 26ECh. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 33ECh. 10.3 - Prob. 34ECh. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.3 - Prob. 37ECh. 10.3 - Prob. 38ECh. 10.3 - Prob. 39ECh. 10.3 - Prob. 40ECh. 10.3 - Prob. 41ECh. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Prob. 49ECh. 10.3 - Prob. 50ECh. 10.3 - Prob. 51ECh. 10.3 - Prob. 52ECh. 10.3 - Prob. 53ECh. 10.3 - Prob. 54ECh. 10.3 - Prob. 55ECh. 10.3 - Prob. 56ECh. 10.3 - Prob. 57ECh. 10.3 - Prob. 58ECh. 10.3 - Prob. 59ECh. 10.3 - Prob. 60ECh. 10.4 - Prob. 1QRCh. 10.4 - Prob. 2QRCh. 10.4 - Prob. 3QRCh. 10.4 - Prob. 4QRCh. 10.4 - Prob. 5QRCh. 10.4 - Prob. 6QRCh. 10.4 - Prob. 7QRCh. 10.4 - Prob. 8QRCh. 10.4 - Prob. 9QRCh. 10.4 - Prob. 10QRCh. 10.4 - Prob. 1ECh. 10.4 - Prob. 2ECh. 10.4 - Prob. 3ECh. 10.4 - Prob. 4ECh. 10.4 - Prob. 5ECh. 10.4 - Prob. 6ECh. 10.4 - Prob. 7ECh. 10.4 - Prob. 8ECh. 10.4 - Prob. 9ECh. 10.4 - Prob. 10ECh. 10.4 - Prob. 11ECh. 10.4 - Prob. 12ECh. 10.4 - Prob. 13ECh. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Prob. 19ECh. 10.4 - Prob. 20ECh. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - Prob. 25ECh. 10.4 - Prob. 26ECh. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.4 - Prob. 30ECh. 10.4 - Prob. 31ECh. 10.4 - Prob. 32ECh. 10.4 - Prob. 33ECh. 10.4 - Prob. 34ECh. 10.4 - Prob. 35ECh. 10.4 - Prob. 36ECh. 10.4 - Prob. 37ECh. 10.4 - Prob. 38ECh. 10.4 - Prob. 39ECh. 10.4 - Prob. 40ECh. 10.4 - Prob. 41ECh. 10.4 - Prob. 42ECh. 10.4 - Prob. 43ECh. 10.4 - Prob. 44ECh. 10.4 - Prob. 45ECh. 10.4 - Prob. 46ECh. 10.4 - Prob. 47ECh. 10.4 - Prob. 48ECh. 10.4 - Prob. 49ECh. 10.4 - Prob. 50ECh. 10.4 - Prob. 51ECh. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.4 - Prob. 54ECh. 10.4 - Prob. 55ECh. 10.4 - Prob. 56ECh. 10.5 - Prob. 1QRCh. 10.5 - Prob. 2QRCh. 10.5 - Prob. 3QRCh. 10.5 - Prob. 4QRCh. 10.5 - Prob. 5QRCh. 10.5 - Prob. 6QRCh. 10.5 - Prob. 7QRCh. 10.5 - Prob. 8QRCh. 10.5 - Prob. 9QRCh. 10.5 - Prob. 10QRCh. 10.5 - Prob. 1ECh. 10.5 - Prob. 2ECh. 10.5 - Prob. 3ECh. 10.5 - Prob. 4ECh. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Prob. 13ECh. 10.5 - Prob. 14ECh. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - Prob. 21ECh. 10.5 - Prob. 22ECh. 10.5 - Prob. 23ECh. 10.5 - Prob. 24ECh. 10.5 - Prob. 25ECh. 10.5 - Prob. 26ECh. 10.5 - Prob. 27ECh. 10.5 - Prob. 28ECh. 10.5 - Prob. 29ECh. 10.5 - Prob. 30ECh. 10.5 - Prob. 31ECh. 10.5 - Prob. 32ECh. 10.5 - Prob. 33ECh. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Prob. 37ECh. 10.5 - Prob. 38ECh. 10.5 - Prob. 39ECh. 10.5 - Prob. 40ECh. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - Prob. 47ECh. 10.5 - Prob. 48ECh. 10.5 - Prob. 49ECh. 10.5 - Prob. 50ECh. 10.5 - Prob. 51ECh. 10.5 - Prob. 52ECh. 10.5 - Prob. 55ECh. 10.5 - Prob. 56ECh. 10.5 - Prob. 59ECh. 10.5 - Prob. 60ECh. 10 - Prob. 1RECh. 10 - Prob. 2RECh. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - Prob. 21RECh. 10 - Prob. 22RECh. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Prob. 25RECh. 10 - Prob. 26RECh. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Prob. 31RECh. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - Prob. 47RECh. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - Prob. 52RECh. 10 - Prob. 53RECh. 10 - Prob. 54RECh. 10 - Prob. 55RECh. 10 - Prob. 56RECh. 10 - Prob. 57RECh. 10 - Prob. 58RECh. 10 - Prob. 59RECh. 10 - Prob. 60RECh. 10 - Prob. 61RECh. 10 - Prob. 62RECh. 10 - Prob. 63RECh. 10 - Prob. 64RECh. 10 - Prob. 65RECh. 10 - Prob. 66RECh. 10 - Prob. 67RECh. 10 - Prob. 68RECh. 10 - Prob. 69RECh. 10 - Prob. 70RECh. 10 - Prob. 71RECh. 10 - Prob. 72RE
Knowledge Booster
Similar questions
- i need help please . and please dont use chat gpt i am trying to learn and see the mistake i did when solving minearrow_forwardThe radius of a sphere decreases at a rate of 3 m/s. Find the rate at which the surface area decreases when the radius is 8 m. Answer exactly or round to 2 decimal places. The surface area decreases at a rate of m²/sarrow_forwardi need help pleasearrow_forward
- (#1) Consider the solid bounded below by z = x² and above by z = 4-y². If we were to project this solid down onto the xy-plane, you should be able to use algebra to determine the 2D region R in the xy-plane for the purposes of integration. Which ONE of these limite of integration would correctly describe R? (a) y: x24x: -22 - (b) y: 22 x: 04-y² (c) y: -√√4-x2. →√√4x²x: −2 → 2 (d) z: 24-y² y: -2 → 2 (e) None of the abovearrow_forwardX MindTap - Cenxxxx Answered: tat "X A 26308049 X 10 EKU-- SP 25: X E DNA Sequenc X b/ui/evo/index.html?elSBN=9780357038406&id=339416021&snapshotid=877369& GE MINDTAP , Limits, and the Derivative 40. Answer 5 4-5 t-10 5 f(x) = 2x - 4 if x ≤0 if x 0 10 ++ -4-3-2-1 f(x) = MacBook Pro Search or type URL 5 1234 x² +1 if x = 0 if x = 0 +arrow_forwardMindTap - Cemy X Answered: tat x A 26308049 × 10 EKU--SP 25:11 × E DNA Sequence x H. pylori index.html?elSBN=9780357038406&id=339416021&snapshotid=877369& NDTAP and the Derivative 41. 42. Answer 12 Ay 5 + -10-5 5 10 -5- f(x) = x +5 if x ≤ 0 -x²+5 if x > 0 to -5 5. 5 f(x) = |x − 1| MacBook Pro AAarrow_forward
- Mind Tap - Cenxxx Answered: tat X A 26308049 × 10 EKU-- SP 25: X E DNA Sequence x H. pylor vo/index.html?elSBN=9780357038406&id=339416021&snapshotld=877369& MINDTAP its, and the Derivative 44. Answer 5 X -10-5 5 10 -5. f(x) = 2 + x +5 if x 0 3 4 f(x) = x² - 1 x+1 if x = -1 MacBook Pro G Search or type URL if x = -1 + AA aarrow_forwardCalculus lll May I please have an explanation of the multivariable chain rule in the example given? Thank youarrow_forwardMind Tap - Cenxxx Answered: tat X A 26308049 X 10 EKU-- SP 25:1 x E DNA Sequence x H. pyl /nb/ui/evo/index.html?elSBN 9780357038406&id=339416021&snapshotid=877369& ⭑ SAGE MINDTAP a ons, Limits, and the Derivative 吃 AA In Exercises 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, and 56, find the values of x for which each function is continuous. 45. f(x) = 2x²+x-1 Answer▾ 46. f(x) = x³- 2x²+x-1 47. f(x) 2 = x²+1 Answer 48. f(x) = 49. f(x) = Answer 50. f(x) = 51. f(x) = I 2x²+1 2 2x - 1 x+1 x-1 2x + 1 x²+x-2 Answer↓ 52. f(x)= = x-1 x2+2x-3 53. $ % MacBook Proarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning