PRECALCULUS:GRAPHICAL,...-NASTA ED.
10th Edition
ISBN: 9780134672090
Author: Demana
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Expert Solution & Answer
Chapter 10.3, Problem 44E
Solution
(a)
To calculate: The percentage of the 2015 ACT scores which are higher than 27.
The percentage of ACT scores higher than 27 is approximately is 16%.
Given:
The mean ACT Math score is 20.9.
The standard deviation of the ACT Math score
The distribution of the population of ACT Math scores is
Concept used:
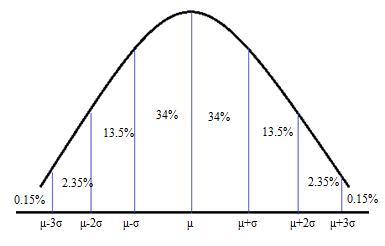
In a normal distribution, the percentage of data within one standard deviation of the mean is about 68%, the percentage of data within two standard deviations of the mean is about 95%, and the percentage of data within three standard deviations of the mean is about 99.7%. The Z score of a data value is the number of standard deviations from the mean and is calculated using the formula
where
Calculation:
The given data point is 27 and its Z score is calculated as shown below
Approximately the score of 27 is one standard deviation more than the mean. With reference to the empirical rule, there is 68% of data within one standard deviation of the mean or there is 34% of the data between the mean and one standard deviation above the mean. Mean divides the entire data into two equal parts 50%, thus the percentage of data above 27 or above one standard deviation is
Conclusion:
The percentage of ACT Math scores higher than 27 is about 16%.
(b)
To calculate: The Math score needed to rank in the top 2.5% of all students who took the test.
The Math score needed to rank in the top 2.5% of all students who took the test is 32.9.
Calculation:
With reference to the normal curve and empirical rule, there is about 95% of data within two standard deviation of the mean and about 2.5% of data in each tail.
Thus top 2.5% of data will be over the two standard deviations above the mean and is calculated as shown below
Approximately the score of 32.9 is two standard deviations above the mean which has the top 2.5% of the students who took the test.
Conclusion:A score of 32.9 is needed to be the top 2.5% of all students who took the test.
(c)
To explain: Whether average ACT score of 50 states is a good estimate of the population mean ACT score.
The average of 50 states’ ACT scores is a good estimate of the population mean ACT score.
Concept used:According to central limit theorem irrespective of the distribution of population, the distribution of sample means will be approximately normal when the sample size is large (greater than 30). The mean of the sample is approximately considered the same as the population mean.
Interpretation:
With reference to the central limit theorem, as the number of states is 50, the sample size is considered to be large and the distribution of the sampling means is approximately normal. Thus the sample mean calculated by adding 50 states’ mean ACT scores and dividing by 50 will be a good estimate of the population mean ACT scores.
Chapter 10 Solutions
PRECALCULUS:GRAPHICAL,...-NASTA ED.
Ch. 10.1 - Prob. 1QRCh. 10.1 - Prob. 2QRCh. 10.1 - Prob. 3QRCh. 10.1 - Prob. 4QRCh. 10.1 - Prob. 5QRCh. 10.1 - Prob. 6QRCh. 10.1 - Prob. 7QRCh. 10.1 - Prob. 8QRCh. 10.1 - Prob. 9QRCh. 10.1 - Prob. 10QR
Ch. 10.1 - Prob. 1ECh. 10.1 - Prob. 2ECh. 10.1 - Prob. 3ECh. 10.1 - Prob. 4ECh. 10.1 - Prob. 5ECh. 10.1 - Prob. 6ECh. 10.1 - Prob. 7ECh. 10.1 - Prob. 8ECh. 10.1 - Prob. 9ECh. 10.1 - Prob. 10ECh. 10.1 - Prob. 11ECh. 10.1 - Prob. 12ECh. 10.1 - Prob. 13ECh. 10.1 - Prob. 14ECh. 10.1 - Prob. 15ECh. 10.1 - Prob. 16ECh. 10.1 - Prob. 17ECh. 10.1 - Prob. 18ECh. 10.1 - Prob. 19ECh. 10.1 - Prob. 20ECh. 10.1 - Prob. 21ECh. 10.1 - Prob. 22ECh. 10.1 - Prob. 23ECh. 10.1 - Prob. 24ECh. 10.1 - Prob. 25ECh. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - Prob. 28ECh. 10.1 - Prob. 29ECh. 10.1 - Prob. 30ECh. 10.1 - Prob. 31ECh. 10.1 - Prob. 32ECh. 10.1 - Prob. 33ECh. 10.1 - Prob. 34ECh. 10.1 - Prob. 35ECh. 10.1 - Prob. 36ECh. 10.1 - Prob. 37ECh. 10.1 - Prob. 38ECh. 10.1 - Prob. 39ECh. 10.1 - Prob. 40ECh. 10.1 - Prob. 41ECh. 10.1 - Prob. 42ECh. 10.1 - Prob. 43ECh. 10.1 - Prob. 44ECh. 10.1 - Prob. 45ECh. 10.1 - Prob. 46ECh. 10.1 - Prob. 47ECh. 10.1 - Prob. 48ECh. 10.1 - Prob. 49ECh. 10.1 - Prob. 50ECh. 10.1 - Prob. 51ECh. 10.1 - Prob. 52ECh. 10.1 - Prob. 53ECh. 10.1 - Prob. 54ECh. 10.1 - Prob. 55ECh. 10.1 - Prob. 56ECh. 10.1 - Prob. 57ECh. 10.1 - Prob. 58ECh. 10.1 - Prob. 59ECh. 10.1 - Prob. 60ECh. 10.1 - Prob. 61ECh. 10.1 - Prob. 62ECh. 10.2 - Prob. 1QRCh. 10.2 - Prob. 2QRCh. 10.2 - Prob. 3QRCh. 10.2 - Prob. 4QRCh. 10.2 - Prob. 5QRCh. 10.2 - Prob. 6QRCh. 10.2 - Prob. 7QRCh. 10.2 - Prob. 8QRCh. 10.2 - Prob. 9QRCh. 10.2 - Prob. 10QRCh. 10.2 - Prob. 1ECh. 10.2 - Prob. 2ECh. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - Prob. 12ECh. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - Prob. 15ECh. 10.2 - Prob. 16ECh. 10.2 - Prob. 17ECh. 10.2 - Prob. 18ECh. 10.2 - Prob. 19ECh. 10.2 - Prob. 20ECh. 10.2 - Prob. 21ECh. 10.2 - Prob. 22ECh. 10.2 - Prob. 23ECh. 10.2 - Prob. 24ECh. 10.2 - Prob. 25ECh. 10.2 - Prob. 26ECh. 10.2 - Prob. 27ECh. 10.2 - Prob. 28ECh. 10.2 - Prob. 29ECh. 10.2 - Prob. 30ECh. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - Prob. 35ECh. 10.2 - Prob. 36ECh. 10.2 - Prob. 37ECh. 10.2 - Prob. 38ECh. 10.2 - Prob. 39ECh. 10.2 - Prob. 40ECh. 10.2 - Prob. 41ECh. 10.2 - Prob. 42ECh. 10.2 - Prob. 43ECh. 10.2 - Prob. 44ECh. 10.2 - Prob. 45ECh. 10.2 - Prob. 46ECh. 10.2 - Prob. 47ECh. 10.2 - Prob. 48ECh. 10.3 - Prob. 1QRCh. 10.3 - Prob. 2QRCh. 10.3 - Prob. 3QRCh. 10.3 - Prob. 4QRCh. 10.3 - Prob. 5QRCh. 10.3 - Prob. 6QRCh. 10.3 - Prob. 7QRCh. 10.3 - Prob. 8QRCh. 10.3 - Prob. 9QRCh. 10.3 - Prob. 10QRCh. 10.3 - Prob. 1ECh. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - Prob. 17ECh. 10.3 - Prob. 18ECh. 10.3 - Prob. 19ECh. 10.3 - Prob. 20ECh. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - Prob. 24ECh. 10.3 - Prob. 25ECh. 10.3 - Prob. 26ECh. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 33ECh. 10.3 - Prob. 34ECh. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.3 - Prob. 37ECh. 10.3 - Prob. 38ECh. 10.3 - Prob. 39ECh. 10.3 - Prob. 40ECh. 10.3 - Prob. 41ECh. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Prob. 49ECh. 10.3 - Prob. 50ECh. 10.3 - Prob. 51ECh. 10.3 - Prob. 52ECh. 10.3 - Prob. 53ECh. 10.3 - Prob. 54ECh. 10.3 - Prob. 55ECh. 10.3 - Prob. 56ECh. 10.3 - Prob. 57ECh. 10.3 - Prob. 58ECh. 10.3 - Prob. 59ECh. 10.3 - Prob. 60ECh. 10.4 - Prob. 1QRCh. 10.4 - Prob. 2QRCh. 10.4 - Prob. 3QRCh. 10.4 - Prob. 4QRCh. 10.4 - Prob. 5QRCh. 10.4 - Prob. 6QRCh. 10.4 - Prob. 7QRCh. 10.4 - Prob. 8QRCh. 10.4 - Prob. 9QRCh. 10.4 - Prob. 10QRCh. 10.4 - Prob. 1ECh. 10.4 - Prob. 2ECh. 10.4 - Prob. 3ECh. 10.4 - Prob. 4ECh. 10.4 - Prob. 5ECh. 10.4 - Prob. 6ECh. 10.4 - Prob. 7ECh. 10.4 - Prob. 8ECh. 10.4 - Prob. 9ECh. 10.4 - Prob. 10ECh. 10.4 - Prob. 11ECh. 10.4 - Prob. 12ECh. 10.4 - Prob. 13ECh. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Prob. 19ECh. 10.4 - Prob. 20ECh. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - Prob. 25ECh. 10.4 - Prob. 26ECh. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.4 - Prob. 30ECh. 10.4 - Prob. 31ECh. 10.4 - Prob. 32ECh. 10.4 - Prob. 33ECh. 10.4 - Prob. 34ECh. 10.4 - Prob. 35ECh. 10.4 - Prob. 36ECh. 10.4 - Prob. 37ECh. 10.4 - Prob. 38ECh. 10.4 - Prob. 39ECh. 10.4 - Prob. 40ECh. 10.4 - Prob. 41ECh. 10.4 - Prob. 42ECh. 10.4 - Prob. 43ECh. 10.4 - Prob. 44ECh. 10.4 - Prob. 45ECh. 10.4 - Prob. 46ECh. 10.4 - Prob. 47ECh. 10.4 - Prob. 48ECh. 10.4 - Prob. 49ECh. 10.4 - Prob. 50ECh. 10.4 - Prob. 51ECh. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.4 - Prob. 54ECh. 10.4 - Prob. 55ECh. 10.4 - Prob. 56ECh. 10.5 - Prob. 1QRCh. 10.5 - Prob. 2QRCh. 10.5 - Prob. 3QRCh. 10.5 - Prob. 4QRCh. 10.5 - Prob. 5QRCh. 10.5 - Prob. 6QRCh. 10.5 - Prob. 7QRCh. 10.5 - Prob. 8QRCh. 10.5 - Prob. 9QRCh. 10.5 - Prob. 10QRCh. 10.5 - Prob. 1ECh. 10.5 - Prob. 2ECh. 10.5 - Prob. 3ECh. 10.5 - Prob. 4ECh. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Prob. 13ECh. 10.5 - Prob. 14ECh. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - Prob. 21ECh. 10.5 - Prob. 22ECh. 10.5 - Prob. 23ECh. 10.5 - Prob. 24ECh. 10.5 - Prob. 25ECh. 10.5 - Prob. 26ECh. 10.5 - Prob. 27ECh. 10.5 - Prob. 28ECh. 10.5 - Prob. 29ECh. 10.5 - Prob. 30ECh. 10.5 - Prob. 31ECh. 10.5 - Prob. 32ECh. 10.5 - Prob. 33ECh. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Prob. 37ECh. 10.5 - Prob. 38ECh. 10.5 - Prob. 39ECh. 10.5 - Prob. 40ECh. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - Prob. 47ECh. 10.5 - Prob. 48ECh. 10.5 - Prob. 49ECh. 10.5 - Prob. 50ECh. 10.5 - Prob. 51ECh. 10.5 - Prob. 52ECh. 10.5 - Prob. 55ECh. 10.5 - Prob. 56ECh. 10.5 - Prob. 59ECh. 10.5 - Prob. 60ECh. 10 - Prob. 1RECh. 10 - Prob. 2RECh. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - Prob. 21RECh. 10 - Prob. 22RECh. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Prob. 25RECh. 10 - Prob. 26RECh. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Prob. 31RECh. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - Prob. 47RECh. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - Prob. 52RECh. 10 - Prob. 53RECh. 10 - Prob. 54RECh. 10 - Prob. 55RECh. 10 - Prob. 56RECh. 10 - Prob. 57RECh. 10 - Prob. 58RECh. 10 - Prob. 59RECh. 10 - Prob. 60RECh. 10 - Prob. 61RECh. 10 - Prob. 62RECh. 10 - Prob. 63RECh. 10 - Prob. 64RECh. 10 - Prob. 65RECh. 10 - Prob. 66RECh. 10 - Prob. 67RECh. 10 - Prob. 68RECh. 10 - Prob. 69RECh. 10 - Prob. 70RECh. 10 - Prob. 71RECh. 10 - Prob. 72RE
Knowledge Booster
Similar questions
- nd ave a ction and ave an 48. The domain of f y=f'(x) x 1 2 (= x<0 x<0 = f(x) possible. Group Activity In Exercises 49 and 50, do the following. (a) Find the absolute extrema of f and where they occur. (b) Find any points of inflection. (c) Sketch a possible graph of f. 49. f is continuous on [0,3] and satisfies the following. X 0 1 2 3 f 0 2 0 -2 f' 3 0 does not exist -3 f" 0 -1 does not exist 0 ve tes where X 0 < x <1 1< x <2 2arrow_forwardNumerically estimate the value of limx→2+x3−83x−9, rounded correctly to one decimal place. In the provided table below, you must enter your answers rounded exactly to the correct number of decimals, based on the Numerical Conventions for MATH1044 (see lecture notes 1.3 Actions page 3). If there are more rows provided in the table than you need, enter NA for those output values in the table that should not be used. x→2+ x3−83x−9 2.1 2.01 2.001 2.0001 2.00001 2.000001arrow_forwardFind the general solution of the given differential equation. (1+x)dy/dx - xy = x +x2arrow_forwardEstimate the instantaneous rate of change of the function f(x) = 2x² - 3x − 4 at x = -2 using the average rate of change over successively smaller intervals.arrow_forwardGiven the graph of f(x) below. Determine the average rate of change of f(x) from x = 1 to x = 6. Give your answer as a simplified fraction if necessary. For example, if you found that msec = 1, you would enter 1. 3' −2] 3 -5 -6 2 3 4 5 6 7 Ꮖarrow_forwardGiven the graph of f(x) below. Determine the average rate of change of f(x) from x = -2 to x = 2. Give your answer as a simplified fraction if necessary. For example, if you found that msec = , you would enter 3 2 2 3 X 23arrow_forwardA function is defined on the interval (-π/2,π/2) by this multipart rule: if -π/2 < x < 0 f(x) = a if x=0 31-tan x +31-cot x if 0 < x < π/2 Here, a and b are constants. Find a and b so that the function f(x) is continuous at x=0. a= b= 3arrow_forwardUse the definition of continuity and the properties of limits to show that the function is continuous at the given number a. f(x) = (x + 4x4) 5, a = -1 lim f(x) X--1 = lim x+4x X--1 lim X-1 4 x+4x 5 ))" 5 )) by the power law by the sum law lim (x) + lim X--1 4 4x X-1 -(0,00+( Find f(-1). f(-1)=243 lim (x) + -1 +4 35 4 ([ ) lim (x4) 5 x-1 Thus, by the definition of continuity, f is continuous at a = -1. by the multiple constant law by the direct substitution propertyarrow_forward1. Compute Lo F⚫dr, where and C is defined by F(x, y) = (x² + y)i + (y − x)j r(t) = (12t)i + (1 − 4t + 4t²)j from the point (1, 1) to the origin.arrow_forward2. Consider the vector force: F(x, y, z) = 2xye²i + (x²e² + y)j + (x²ye² — z)k. (A) [80%] Show that F satisfies the conditions for a conservative vector field, and find a potential function (x, y, z) for F. Remark: To find o, you must use the method explained in the lecture. (B) [20%] Use the Fundamental Theorem for Line Integrals to compute the work done by F on an object moves along any path from (0,1,2) to (2, 1, -8).arrow_forwardhelp pleasearrow_forwardIn each of Problems 1 through 4, draw a direction field for the given differential equation. Based on the direction field, determine the behavior of y as t → ∞. If this behavior depends on the initial value of y at t = 0, describe the dependency.1. y′ = 3 − 2yarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning