
Concept explainers
An opaque, diffuse, gray
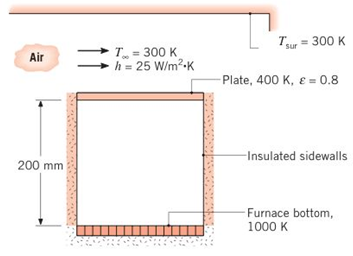
(a) Evaluate the net radiative heat transfer lo the bottom surface of the plate.
(b) If the plate has mass and specific heat of 2 kg and
(c) Extending the analysis of part (b), generate a plot of the change in temperature of the plate with time,
Want to see the full answer?
Check out a sample textbook solution
Chapter 13 Solutions
Fundamentals of Heat and Mass Transfer
- 2. Consider a polymeric membrane within a 6 cm diameter stirred ultrafiltration cell. The membrane is 30 μm thick. The membrane has pores equivalent in size to a spherical molecule with a molecular weight of 100,000, a porosity of 80%, and a tortuosity of 2.5. On the feed side of the membrane, we have a solution containing a protein at a concentration of 8 g L-1 with these properties: a = 3 nm and DAB = 6.0 × 10-7 cm² s¹. The solution viscosity is 1 cP. The hydrodynamic pressure on the protein side of the membrane is 20 pounds per square inch (psi) higher than on the filtrate side of the membrane. Assume that the hydrodynamic pressure difference is much larger than the osmotic pressure difference (advection >> diffusion). Determine the convective flow rate of the solution across the membrane.arrow_forward1. Calculate the filtration flow rate (cm³ s¹) of a pure fluid across a 100 cm² membrane. Assume the viscosity (µ) of the fluid is 1.8 cP. The porosity of the membrane is 40% and the thickness of the membrane is 500 μm. The pores run straight through the membrane and these pores have a radius of 0.225 μm. The pressure drop applied across the membrane is 75 psi. (Note: 1 cP = 0.001 N s m²² = 0.001 Pa s.)arrow_forward3. Tong and Anderson (1996) obtained for BSA the following data in a polyacrylamide gel for the partition coefficient (K) as a function of the gel volume fraction (4). The BSA they used had a molecular weight of 67,000, a molecular radius of 3.6 nm, and a diffusivity of 6 × 10-7 cm2 s-1. Compare the Ogston equation K=exp + to their data and obtain an estimate for the radius of the cylindrical fibers (af) that comprise the gel. Hint: You will need to plot Ink as a function of gel volume fraction as part of your analysis. Please include your MATLAB, or other, code with your solution. Gel Volume Fraction (4) KBSA 0.00 1.0 0.025 0.35 0.05 0.09 0.06 0.05 0.075 0.017 0.085 0.02 0.105 0.03arrow_forward
- Assignment 10, Question 1, Problem Book #189 Problem Statement An ideal Brayton cycle operates with no reheat, intercooling, or regeneration. The com- pressor inlet conditions are 30°C and 1 bar. The compression ratio is 11. The turbine inlet temperature is 1,300 K. Determine the turbine exit temperature, the thermal efficiency, and the back work ratio. Use an air standard analysis. Answer Table Correct Stage Description Your Answer Answer * 1 Compressor inlet enthalpy (kJ/kg) Due Date Grade (%) Weight Attempt Action/Message Part Type 1 2 1 Compressor inlet relative pressure 1 Compressor exit relative pressure 1 Compressor exit enthalpy (kJ/kg) Compressor work (kJ/kg) Turbine inlet enthalpy (kJ/kg) Dec 5, 2024 11:59 pm Dec 5, 2024 11:59 pm Dec 5, 2024 11:59 pm 0.0 0.0 1 1/5 Submit Stage 1 0.0 1 1 Dec 5, 2024 11:59 pm 0.0 1 Dec 5, 2024 11:59 pm 0.0 1 2 Turbine inlet relative pressure Dec 5, 2024 11:59 pm Dec 5, 2024 11:59 pm 0.0 1 1/5 0.0 1 2 Combustion chamber heat addition (kJ/kg) Dec…arrow_forwardAssignment 10, Question 4, Problem Book #202 Problem Statement An ideal Brayton cycle with a two-stage compressor, a two-stage turbine, and a regenerator operates with a mass flow rate of 25 kg/s. The regenerator cold inlet is at 490 K and its effectiveness is 60%. Ambient conditions are 90 kPa and 20°C. The intercooler operates at 450 kPa and the reheater operates at 550 kPa. The temperature at the exit of the combustion chamber is 1,400 K. Heat is removed in the intercooler at a rate of 2.5 MW and heat is added in the reheater at a rate of 10 MW. Determine the thermal efficiency and the back work ratio. Use a cold air standard analysis with cp = 1.005 kJ/(kg K) and k = 1.4. . Answer Table Stage Description Your Answer Correct Answer Due Date Grade (%) 1 Thermal efficiency (%) Dec 5, 2024 11:59 pm 0.0 1 Weight Attempt Action/Message 1/5 Part Type Submit 1 Back work ratio (%) Dec 5, 2024 11:59 pm 0.0 1 * Correct answers will only show after due date has passed.arrow_forwardAssignment 10, Question 3, Problem Book #198 Problem Statement Consider a Brayton cycle with a regenerator. The regenerator has an effectiveness of 75%. The compressor inlet conditions are 1.2 bar and 300 K and the mass flowrate is 4.5 kg/s. The compressor outlet pressure is 9 bar. Both the compressor and turbine consist of a single isentropic stage. What minimum power output must be achieved before the regenerator begins to have a benefit? Use an air-standard analysis. Answer Table Correct Answer Stage Description Your Answer Due Date Grade (%) Part Weight Attempt Action/Message Туре 1 Power output (MW) Dec 5, 2024 11:59 pm 0.0 1 1/5 Submit * Correct answers will only show after due date has passed.arrow_forward
- Q-3 Consider an engine operating on the ideal Diesel cycle with air as the working fluid. The volume of the cylinder is 1200 cm³ at the beginning of the Compression process, 75 cm³ at the end, and 150 cm³ after the heat addition process. Air is at 17°c and lookpa at the beginning of the compression proc ess. Determine @ The pressure at the beginning of the heat rejection process. the net work per cycle in kjⒸthe mean effective pressur. Answers @264.3 KN/m² ②0.784 kj or 544-6 kj © 697 KN 19 2 marrow_forwardIn the system shown in the (img 1), water flows through the pump at a rate of 50L/s. The permissible NPSH providedby the manufacturer with that flow is 3.6 m. Determine the maximum height Delta z above the water surface at which the Pump can be installed to operate without cavitation. Include all losses in the suction tube. What is the value of the smaller total losses? What is the value of minor-minor losses? What is the value of major-minor losses?arrow_forwardA plastic canister whose bottom surface can be approximated as a flat surface1.9 m and 3 m long, travels through the water at 19 °C with a speed of up to 48 km/h. Determine: Drag due to friction that water exerts on the boat The power needed to overcome itarrow_forward
- (Fig. 1) shows the performance of a centrifugal pump for various diameters of theimpeller. For such a pump with a 5" diameter impeller, what power, in hp, would be expected to supply 5 L/s?what is its efficiency, in %?A pumping system requires 6 L/s of water with a load of 8 m, which of the pumpsof (fig. 1) would you recommend for this application?;arrow_forwardYou have the following information about a ship (image 1) Determine:a) Calculation of the block coefficient. b) Calculation of the wake coefficient. c) Determine the length of the wake.arrow_forwardA stainless steel canoe moves horizontally along the surface of a lake at 3.7 mi/h. TheThe lake's water temperature is 60°F. The bottom of the canoe is 25 ft long and flat. The boundary layer inThe bottom of the canoe is laminar or turbulent. the value of kinematic viscosity is? the value of the Reynolds number is?arrow_forward
 Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
