Calculus Volume 3
16th Edition
ISBN: 9781938168079
Author: Gilbert Strang, Edwin Jed Herman
Publisher: OpenStax
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 6.3, Problem 133E
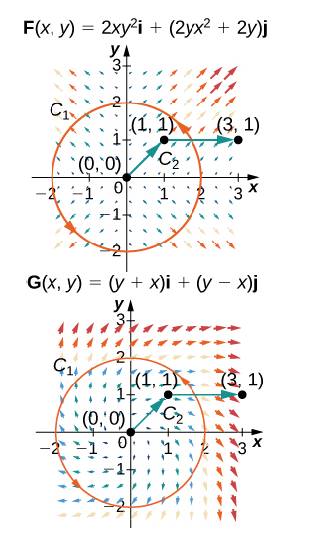
For the following exercises, let F(x, y) = 2xy2i + (2yx2+2y)j and
G(x, y) = (y + x)i + (y — x)j, and let C1be the curve consisting of the circle of radius 2, centered at the origin and oriented counterclockwise, and C2be the curve consisting of a line segment from (0, 0) to (1, 1) followed by a line segment from (1, 1) to (3, 1).
133. Calculate the line
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
13. In 2000, two organizations conducted surveys to ascertain the public's opinion on banning gay men from serving in leadership roles in the Boy Scouts.• A Pew poll asked respondents whether they agreed with "the recent decision by the Supreme Court" that "the Boy Scouts of America have a constitutional right to block gay men from becoming troop leaders."A Los Angeles Times poll asked respondents whether they agreed with the following statement: "A Boy Scout leader should be removed from his duties as a troop leader if he is found out to be gay, even if he is considered by the Scout organization to be a model Boy Scout leader."One of these polls found 36% agreement; the other found 56% agreement. Which of the following statements is true?A) The Pew poll found 36% agreement, and the Los Angeles Times poll found 56% agreement.B) The Pew poll includes a leading question, while the Los Angeles Times poll uses neutral wording.C) The Los Angeles Times Poll includes a leading question, while…
A tank contains 60 kg of salt and 2000 L of water. Pure water enters a tank at the rate 8 L/min. The
solution is mixed and drains from the tank at the rate 11 L/min.
Let y be the number of kg of salt in the tank after t minutes.
The differential equation for this situation would be:
dy
dt
y(0) =
Simplify the below expression.
3 - (-7)
Chapter 6 Solutions
Calculus Volume 3
Ch. 6.1 - The domain of vector field F = F(x, y) is a set of...Ch. 6.1 - For the following exercises, determine whether the...Ch. 6.1 - For the following exercises, determine whether the...Ch. 6.1 - For the following exercises, determine whether the...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...
Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - What is vector field F(x, y) with a value at (x,...Ch. 6.1 - For the following exercises, write formulas for...Ch. 6.1 - For the following exercises, write formulas for...Ch. 6.1 - For the following exercises, write formulas for...Ch. 6.1 - Give a formula F(x, y) = M(x, y)i + N(x, y)j for...Ch. 6.1 - Is vector field F(x, y) = (P(x, y), Q(x, y)) =...Ch. 6.1 - Find a formula for vector field F(x, y) = M(x,,y)i...Ch. 6.1 - For the following exercises, assume that an...Ch. 6.1 - For the following exercises, assume that an...Ch. 6.1 - For the following exercises, assume that an...Ch. 6.1 - c(t) = (sin t. cos t, et); F(x,y,z)=y,x,zCh. 6.1 - For the following exercises, let F = xi + yi, G =...Ch. 6.1 - For the following exercises, let F = xi + yi, G =...Ch. 6.1 - For the following exercises, let F = xi + yi, G =...Ch. 6.1 - For the following exercises, let F = xi + yj, G =...Ch. 6.1 - For the following exercises,...Ch. 6.1 - For the following exercises, let...Ch. 6.1 - For the following exercises, let...Ch. 6.2 - True or False? Line integral cf(x,y)dsis equal to...Ch. 6.2 - True or False? Vector functions r1= ti +t2j,...Ch. 6.2 - True or False? c(Pdx+Qdy)=c(PdxQdy)Ch. 6.2 - True or False? A piecewise smooth cuive C consists...Ch. 6.2 - True or False?If C is given by x(t) = t,y(t) = t,0...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - Evaluate the line integral of scalar function xy...Ch. 6.2 - Find yc2dx+(xy x 2)dy along C: y = 3x from C (0,...Ch. 6.2 - Find yc2dx+(xy x 2)dyalong C: y2= 9x from (0, 0)...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, find the flux. 87....Ch. 6.2 - For the following exercises, find the flux. 88....Ch. 6.2 - For the following exercises, find the flux. 89....Ch. 6.2 - For the following exercises, find the flux. 90....Ch. 6.2 - For the following exercises, find the flux. 91....Ch. 6.2 - Find the line integral of k c z 2dx+ydy+2ydz,where...Ch. 6.2 - A spring is made of a thin wire twisted into the...Ch. 6.2 - A thin wire is bent into the shape of a semicircle...Ch. 6.2 - An object moves in force field...Ch. 6.2 - Find the work done when an object moves in force...Ch. 6.2 - If an inverse force field F. is given by F(x, y,...Ch. 6.2 - David and Sandra plan to evaluate line integral...Ch. 6.3 - True or False? If vector field F is conservative...Ch. 6.3 - Trueor False? Function r(t) = a + t(b — a), where...Ch. 6.3 - True or False? Vector field F(x, y,z) = (y sinz)i...Ch. 6.3 - True or False?Vector field F(x,y,z)= yi + (x + z)j...Ch. 6.3 - Justify the Fundamental Theorem of Line Integrals...Ch. 6.3 - [T] Find cF.dr,,] where...Ch. 6.3 - [T] Evaluate line integral cF.dr, where...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - [T] Let F(x, y, z) = x2i + zsin(yz)j + y sin(yz)k....Ch. 6.3 - [T] Find line integral cF.dr,of vector field F(x,...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - Find the circulation and flux of field F=yi+xj...Ch. 6.3 - Compute ccosxcosydxsinxsinydy, where...Ch. 6.3 - Complete the proof of The Path Independence Test...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - easuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - ]Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, use Green’s theorem....Ch. 6.4 - For the following exercises, use Green’s theorem....Ch. 6.4 - Find the counterclockwise circulation of field...Ch. 6.4 - Evaluate cy3dxx3y2dy,where C is the positively...Ch. 6.4 - Evaluate cy3dxx3dy,where C includes the two...Ch. 6.4 - Calculate cx2ydx+xy2dy,where C isa circle of...Ch. 6.4 - Calculate integral...Ch. 6.4 - Evaluate integral c( x 2+ y 2)dx+2xydy,where C is...Ch. 6.4 - Evaluate line integralc(ysin( y)cos( y)dx+2x sin...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - [T] Evaluate Green’s theorem using a computer...Ch. 6.4 - Evaluate c(x2y2xy+y2)ds,where C is the boundary of...Ch. 6.4 - Evaluate ( y+2)dx+( x1)dyc ( x1 ) 2+ ( y+2 )...Ch. 6.4 - 173. Evaluate xdx+ydy c x 2 + y 2 , . where C is...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - A particle starts at point (-2, 0), moves along...Ch. 6.4 - David and Sandra are skating on a frictionless...Ch. 6.4 - Use Green’s theorem to find the work done by force...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Evaluate line integral c y 2dx+x2dy,where C is...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral c1+...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral c(3y...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Let C be a tiiangulai closed curve from (0, 0) to...Ch. 6.4 - Use Green’s theoiem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate cxydx+ x 3 y 3dy,...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Let F(x,y)=(cos(x5))13y3i+13x3j.Find the...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Let C be the boundary of square 0x,0y, traversed...Ch. 6.4 - Use Green’s theorem to evaluate line integral,...Ch. 6.4 - Use Green’s Theorem to evaluate integial...Ch. 6.4 - Use Green’s theorem in a plane to evaluate line...Ch. 6.4 - Calculate the outward flux of F = -xi + 2yj over a...Ch. 6.4 - 200. [T] Let C be circle x2+ y2= 4 oriented in the...Ch. 6.4 - Find the flux of field F = -xi + yj across x2+ y2...Ch. 6.4 - Let F = (y2— x2)i + (x2+y2)j, and let C be a...Ch. 6.4 - [T] Let C be unit circle x2+ y2 = 1 traversed once...Ch. 6.4 - [T] Find the outward flux of vector field F = xy2i...Ch. 6.4 - Consider region R bounded by parabolas y= x2and x...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - 233.w(x,y,z)=(x2+y2+z2)1/2Ch. 6.5 - 232.u(x,y,z)=ex(cosysiny)...Ch. 6.5 - 234.IfF(x,y,z)=2i+2xj+3ykCh. 6.5 - ...Ch. 6.5 - Find div F, given that F = f, where f(x,y,z)=xy3z2...Ch. 6.5 - 237. Find the divergence of F for vector field...Ch. 6.5 - Find the divergence of F for vector field...Ch. 6.5 - For the following exercises, use r = |r|and r =...Ch. 6.5 - For the following exercises, use r = |r|and r =...Ch. 6.5 - For the following exercises, use r = |r|and r =...Ch. 6.5 - For the following exercises, use r = |r| and r =...Ch. 6.5 - For the following exercises, use a computer...Ch. 6.5 - For the following exercises, use a computer...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, consider a rigid body...Ch. 6.5 - For the following exercises, consider a rigid body...Ch. 6.5 - For the following exercises, consider a rigid body...Ch. 6.5 - In the following exercises, suppose that F=0 and...Ch. 6.5 - In the following exercises, suppose that F=0 and...Ch. 6.5 - In the following exercises, suppose a solid object...Ch. 6.5 - In the following exercises, suppose a solid object...Ch. 6.5 - Consider rotational velocity field v=0,10z,-10y....Ch. 6.6 - For the following exercises, determine whether the...Ch. 6.6 - wFor the following exercises, determine whether...Ch. 6.6 - For the following exercises, determine whether the...Ch. 6.6 - For the following exercises, determine whether the...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, use a computer...Ch. 6.6 - For the following exercises, use a computer...Ch. 6.6 - For the following exercises, let S be the...Ch. 6.6 - For the following exercises, let S be the...Ch. 6.6 - For the following exercises, let S be the...Ch. 6.6 - wFor the following exercises, evaluate sFNds for...Ch. 6.6 - For the following exercises, evaluate sFNds for...Ch. 6.6 - For the following exercises, evaluate sFNds for...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - wFor the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, use geometric...Ch. 6.6 - For the following exercises, use geometric...Ch. 6.6 - For the following exercises, use geometric...Ch. 6.6 - A lamina has the shape of a portion of sphere...Ch. 6.6 - A lamina has the shape of a portion of sphere...Ch. 6.6 - A paper cup has the shape of an inverted right...Ch. 6.6 - For the following exercises, the heat flow vector...Ch. 6.6 - For the following exercises, the heat flow vector...Ch. 6.6 - For the following exercises, consider the radial...Ch. 6.6 - For the following exercises, consider the radial...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following application exercises, the goal...Ch. 6.7 - For the following application exercises, the goal...Ch. 6.7 - For the following application exercises, the goal...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a CAS along with...Ch. 6.8 - For the following exercises, use a CAS along with...Ch. 6.8 - For the following exercises, use a CAS along with...Ch. 6.8 - `For the following exercises, use a CAS along with...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, Fourier’s law of heat...Ch. 6.8 - For the following exercises, Fourier’s law of heat...Ch. 6.8 - For the following exercises, Fourier’s law of heat...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - Draw the following vector fields. 431....Ch. 6 - Draw the following vector fields. 432....Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Evaluate the following integrals. 437....Ch. 6 - Evaluate the following integrals. 438. Cydx+xy2dy...Ch. 6 - Evaluate the following integrals. 439. Sxy2dS ,...Ch. 6 - Find the divergence and curl for the following...Ch. 6 - Find the divergence and curl for the following...Ch. 6 - Use Green’s theorem to evaluate the following...Ch. 6 - Use Green’s theorem to evaluate the following...Ch. 6 - Use Stokes’ theorem to evaluate ScurlFdS . 444....Ch. 6 - Use Stokes’ theorem to evaluate ScurlFdS . 445....Ch. 6 - Use the divergence theorem to evaluate SFdS . 446....Ch. 6 - Use the divergence theorem to evaluate SFdS . 447....Ch. 6 - Find the amount of work perfumed by a 50 -kg woman...Ch. 6 - Find the total mass of a thin wire in the shape of...Ch. 6 - Find the total mass of a thin sheet in the shape...Ch. 6 - Use the divergence theorem to compute the value of...
Additional Math Textbook Solutions
Find more solutions based on key concepts
2. Probability Rewrite the following statement so that the likelihood of rain is expressed as a value between 0...
Elementary Statistics (13th Edition)
Expanding circle The area of a circle increases at a rate of 1 cm2/s. a. How fast is the radius changing when t...
Calculus: Early Transcendentals (2nd Edition)
TRY IT YOURSELF 1
Find the mean of the points scored by the 51 winning teams listed on page 39.
Elementary Statistics: Picturing the World (7th Edition)
Show that 34=12 using each of the following models. a. Repeated-addition number line b. Rectangular array c. Ar...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Twenty five people, consisting of 15 women and 10 men are lined up in a random order. Find the probability that...
A First Course in Probability (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Already got wrong chatgpt answer Plz don't use chatgpt answer will upvote otherwise leave it .arrow_forwardy=f'(x) 1 8 The function f is defined on the closed interval [0,8]. The graph of its derivative f' is shown above. How many relative minima are there for f(x)? O 2 6 4 00arrow_forward60! 5!.7!.15!.33!arrow_forward
- Use Euler's summation formula to prove that, for x > 2, Σ log n n3 = A log x 2x2 n≤x where A is a constant. - 1 +0 4x2 log x x3 "arrow_forward• • Let > be a potential for the vector field F = (−2 y³, −6 xy² − 4 z³, −12 yz² + 4 2). Then the value of sin((-1.63, 2.06, 0.57) – (0,0,0)) is - 0.336 -0.931 -0.587 0.440 0.902 0.607 -0.609 0.146arrow_forward1. If f(x² + 1) = x + 5x² + 3, what is f(x² - 1)?arrow_forward
- 2. What is the total length of the shortest path that goes from (0,4) to a point on the x-axis, then to a point on the line y = 6, then to (18.4)?arrow_forwardThe value of cos(4M) where M is the magnitude of the vector field with potential ƒ = e² sin(лy) cos(π²) at x = 1, y = 1/4, z = 1/3 is 0.602 -0.323 0.712 -0.816 0.781 0.102 0.075 0.013arrow_forwardThere is exactly number a and one number b such that the vector field F = conservative. For those values of a and b, the value of cos(a) + sin(b) is (3ay + z, 3ayz + 3x, −by² + x) is -0.961 -0.772 -1.645 0.057 -0.961 1.764 -0.457 0.201arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY