
a.
Show that the area of the triangle is
a.
Answer to Problem 65E
Area of triangle
Here,
Explanation of Solution
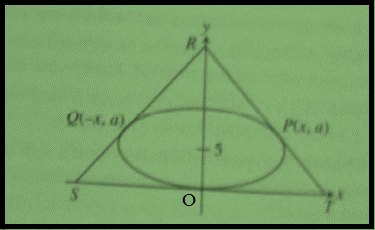
Given:
Ellipse of equation:
A triangle

Concept Used:
The equation of tangent line that passes through the point
Here,
Calculation:
Rewrite the equation
First Derivative:-
Take
Also,
Slope of ellipse :
Slope of ellipse at point
Take point
As, given that point
Put
Slope: - of ellipse passes through point
The x -intercept of line: -
Since, the value of
For x −intercept put
So,
And the co-ordinates of vertex
And, the distance of
And,
The
Since, the value of
For
So,
And the co-ordinates of vertex
The distance of
Also,
Area:-
Area of triangle
So, Area of triangle
Area of triangle
Area of triangle
Area of triangle
But,
Area of triangle
Put
Area of triangle
Here,
Conclusion:
Area of triangle
Here,
b.
To Find: the domain of
b.
Explanation of Solution
Given:
Area of triangle
Here,
Calculation:
Rewrite the area,
Area of triangle
Here,
Area is defined if
On solving,
So, Domain:
Graph:
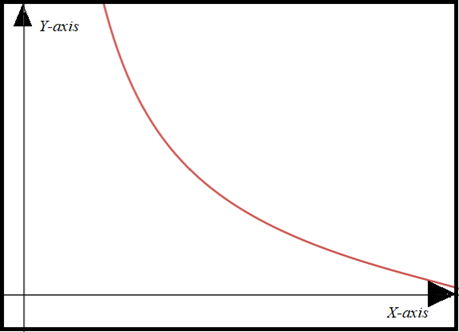
Here,
According to graph, the asymptotes of graph does not form triangle as tangent lines formed in given problem.
The vertical asymptote is
c.
Find the height of the triangle with minimum area.
Also, check if it is related to the y-coordinate of the center of the ellipse.
c.
Answer to Problem 65E
Height
Also, height is related to the y-coordinate of the center of the ellipse. It is the triple time of the y-coordinate of the center of the ellipse.
Explanation of Solution
Given:
Area of triangle
Here,
Calculation:
Differentiate the
For point of minima put
Height
Put the value and solve,
Height
Conclusion:
Height
Also, height is related to the y-coordinate of the center of the ellipse. It is the triple time of the y-coordinate of the center of the ellipse.
d.
Repeat the part (a) to (c) for the ellipse
d.
Answer to Problem 65E
Area of triangle
Domain:
Explanation of Solution
Given:
From part (a)
Area of triangle
Here,
Calculation:
Solve in the same way as part (a), (b) and (c).
Area of triangle
Here,
Domain:
Since, Graph Is same for both parts. So,
Graph:
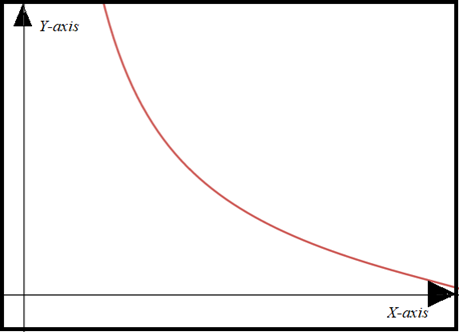
Here,
Chapter 4 Solutions
Advanced Placement Calculus Graphical Numerical Algebraic Sixth Edition High School Binding Copyright 2020
- Find the equation of the tangent line to the graph of the given function at the given value of x. 6 f(x) = x(x² - 4x+5)*; x=2arrow_forwardFind the equation of the tangent line to the graph of the given function at the given value of x. f(x)=√√x+33; x=4arrow_forwardFind g[f(-7)]. f(x) = x² + 1; g(x)=-5x-1arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





