
(a)
To find: The equation of the volume.
(a)
Answer to Problem 50RE
The required expression for volume is
Explanation of Solution
Given information:
The piece of cardboard is
Calculation:
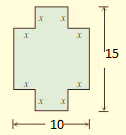
The height of the prism can be x, which is the labeled length of the rectangle next to the base and lid.
In order to write a formula in terms of the variable x, it is required to write expressions for the length, width, and height of the box.
It can be said that the length is the bottom of the base the prism. To find this value, we can subtract
The width is the side of the base of the prism. To find this value, we can subtract
The volume of the rectangular box is given by:
Substitute the value of length width and height gives:
This is the required expression for volume.
(b)
To find: The domain of
(b)
Answer to Problem 50RE
The required domain is
Explanation of Solution
Given information:
The required expression for volume is
Calculation:
Let the height of the prism be
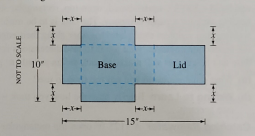
In order to write a formula in terms of the variable
It can be said that the length is the bottom of the base of the prism. To find this value, we can subtract x and x from 10 and divide this by 2, since there are two equal rectangles (base and lid).
The width is the side of the base of the prism. To find this value, we can subtract
The domain of the volume is where
Combining these requirements the domain is
(c)
To find: Use the graphical method to find the maximum value of
(c)
Answer to Problem 50RE
It is observed from the graph that the maximum volume is 66.02 is at
Explanation of Solution
Given information:
The volume function is
Calculation:
In order to draw the graph of volume function substitute different values of
Let
The point will be
Similarly, more point can be found and plot the on the graph. The graph is given below:
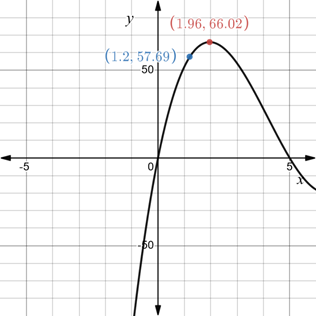
It is observed from the graph that the maximum volume is 66.02 is at
(c)
To find: confirm your result in part (c) analytically.
(c)
Answer to Problem 50RE
It is found analytically that the maximum volume is 66.02 is at
Explanation of Solution
Given information:
Volume function is
Calculation:
In order to solve the equation
In order to find the maximum value, it is required to find the critical points.
In order to find critical points differentiate volume function with respect to
Now substitute
Use quadratic formula
Discard the largest value because it is not in the domain
Perform second order derivative test to check whether the volume is maximum.
Now differentiate again
Now find maximum value of volume by substituting
This proves that the volume is maximum at
Chapter 4 Solutions
Advanced Placement Calculus Graphical Numerical Algebraic Sixth Edition High School Binding Copyright 2020
- 4. The revenue (in thousands of dollars) from producing x units of an item is R(x)=8x-0.015 x². a) Find the average rate of change of revenue when the production is increased from 1000 to 1001 units.arrow_forwardMATH 122 WORKSHEET 3 February 5, 2025 . Solve the following problems on a separate sheet. Justify your answers to earn full credit. 1. Let f(x) = x² - 2x + 1. (a) Find the slope of the graph of y = f (x) at the point P = (0,1) by directly evaluating the limit: f'(0) = lim ( f(Ax) - f(0) Ax Ax→0 (b) Find the equation of the tangent line 1 to the graph of ƒ at P. What are the x and y intercepts of 1 ? (c) Find the equation of the line, n, through P that is perpendicular to the tangent line l. (Line n is called the normal line to the graph of f at P.) (d) Sketch a careful graph that displays: the graph of y = f (x), its vertex point, its tangent and normal lines at point P, and the x and y intercepts of these lines. Bonus: Find the coordinates of the second point, Q, (QP), at which the normal line n intersects the graph of f. 2. A rock is thrown vertically upward with an initial velocity of 20 m/s from the edge of a bridge that is 25 meters above a river bed. Based on Newton's Laws of…arrow_forward3. Use the graph for problem #35, p175 to answer the questions. The average price (in cents) per gallon of unleaded gasoline in the United States for the years 2010 to 2019 is shown in this chart. Find the average rate of change per year in the average price per gallon for each time period. Source: U.S. Energy Information Administration. a) 2010 to 2013 b) 2012 to 2018 c) 2014 to 2019arrow_forward
- 4. Researchers at Iowa State University and the University of Arkansas have developed a piecewise function that can be used to estimate the body weight (in grams) of a male broiler during the first 56 days of life according to W(t)=48+3.64t+0.6363²+0.00963 t³ if 1St≤28, -1004+65.8t if 28arrow_forward3. Given the function h(x)=(x²+x-12 if x≤1 3-x if x>1' a) Graph the function h(x). Make the graph big enough to be easily read using the space below. Be sure to label all important aspects of the graph. b) Find all values of x where the function is discontinuous. c) Find the limit from the left and from the right at any values of x found in part b.arrow_forward2. Find the instantaneous rate of change for each function f(x)=2x²-x+3 at x=0..arrow_forward4x-3 2. Determine the interval over which the function is continuous. x+4arrow_forward1. Find the average rate of change for the following functions over the given intervals. a) f(x)=4x-2x²+3x between x=-1 and x=4 b) y lnx between x=1 and x=4arrow_forward1. Find all values x=a where the function is discontinuous, determine if the discontinuity is removable or non- removable. For each value of x, give the limit of the function as x approaches a. Be sure to note when the limit doesn't exist and explain how you know. a) f(x)= 2-x x²(x+5) b) f(x)= x²-9x x²+3x c) p(x)=-3x²+2x²+5x-8arrow_forwardDo the Laplace Transformation and give the answer in Partial Fractions. Also do the Inverted Laplace Transformation and explain step-by-step.arrow_forward12. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.508.XP. ASK YOUR TEA Make a substitution to express the integrand as a rational function and then evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) x + 16 dx X Need Help? Read It SUBMIT ANSWER 13. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.512.XP. ASK YOUR TEA Make a substitution to express the integrand as a rational function and then evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) dx 8)(2x + 1) Need Help? Read It SUBMIT ANSWER 14. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.518.XP. Find the area of the region under the given curve from 1 to 5. y = x² +7 6x - x² Need Help? Read It ASK YOUR TEAarrow_forwardDETAILS MY NOTES SESSCALCET2 6.3.012. 6. [-/1 Points] Evaluate the integral. x-4 dx x² - 5x + 6 Need Help? Read It SUBMIT ANSWER 7. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.019. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) x²+1 (x-6)(x-5)² dx Need Help? Read It SUBMIT ANSWER 8. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.021. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) ✓ x² 4 +4 dxarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





