Chapter 4, Problem 12RE

a.

To determine

To identify: The interval in which the function $y=\sin 3x+\cos 4x,0\le x\le 2\pi$ is increasing.

Answer to Problem 12RE

The function is increasing in the interval $\left(0,0.176\right)$ , $\left(0.994,1.57\right)$ , $\left(2.148,2.965\right)$ , $\left(3.834,\frac{3\pi }{2}\right)$ , $\left(5.591,2\pi \right)$ .

Explanation of Solution

Given information:

The given function is $y=\sin 3x+\cos 4x,0\le x\le 2\pi$

Consider the given function.

Calculate the derivative of the function.

  $\frac{dy}{dx}=3\cos 3x-4\sin 4x$

Now determine the critical points.

By putting $\frac{dy}{dx}=0$ .

  $\begin{array}{c}0=3\cos 3x-4\sin 4x\\ \cos 3x=\frac{4}{3}\sin 4x\end{array}$

So, the critical points are:

  $x\approx 0.176,x\approx 0.994,x\approx 1.57,x\approx 2.148,x\approx 2.965,x\approx 3.834,x=\frac{3\pi }{2},x\approx 5.591$

Now draw the table 1:

Intervals	$\left(0,0.176\right)$	$\left(0.176,0.994\right)$	$\left(0.994,1.57\right)$	$\left(1.57,2.148\right)$	$\left(2.148,2.965\right)$
Sign of derivative	$+$	$-$	$+$	$-$	$+$
Behavior of y	Increasing	Decreasing	Increasing	Decreasing	Increasing
Intervals	$\left(2.965,3.834\right)$	$\left(3.834,\frac{3\pi }{2}\right)$	$\left(\frac{3\pi }{2},5.591\right)$	$\left(5.591,2\pi \right)$
Sign of derivative	$-$	$+$	$-$	$+$
Behavior of y	Decreasing	Increasing	Decreasing	Increasing

Thus, from the table 1 it can be observed that the function is increasing in the interval $\left(0,0.176\right)$ , $\left(0.994,1.57\right)$ , $\left(2.148,2.965\right)$ , $\left(3.834,\frac{3\pi }{2}\right)$ , $\left(5.591,2\pi \right)$ .

b.

To determine

To identify: The interval in which the function $y=\sin 3x+\cos 4x,0\le x\le 2\pi$ is decreasing.

Answer to Problem 12RE

The function is decreasing in the interval $\left(0.176,0.994\right)$ , $\left(1.57,2.148\right)$ , $\left(2.965,3.834\right)$ , $\left(\frac{3\pi }{2},5.591\right)$ .

Explanation of Solution

Given information:

The given function is $y=\sin 3x+\cos 4x,0\le x\le 2\pi$

Consider the given function.

It is known that the table 1 is

Intervals	$\left(0,0.176\right)$	$\left(0.176,0.994\right)$	$\left(0.994,1.57\right)$	$\left(1.57,2.148\right)$	$\left(2.148,2.965\right)$
Sign of derivative	$+$	$-$	$+$	$-$	$+$
Behavior of y	Increasing	Decreasing	Increasing	Decreasing	Increasing
Intervals	$\left(2.965,3.834\right)$	$\left(3.834,\frac{3\pi }{2}\right)$	$\left(\frac{3\pi }{2},5.591\right)$	$\left(5.591,2\pi \right)$
Sign of derivative	$-$	$+$	$-$	$+$
Behavior of y	Decreasing	Increasing	Decreasing	Increasing

Thus, from the table 1 it can be observed that the function is decreasing in the interval $\left(0.176,0.994\right)$ , $\left(1.57,2.148\right)$ , $\left(2.965,3.834\right)$ , $\left(\frac{3\pi }{2},5.591\right)$ .

c.

To determine

To identify: The interval in which the function $y=\sin 3x+\cos 4x,0\le x\le 2\pi$ is concave up.

Answer to Problem 12RE

The function is concave up in the interval $\left(0.542,1.266\right)$ , $\left(1.876,2.6\right)$ , $\left(3.425,4.281\right)$ , $\left(5.144,6\right)$ .

Explanation of Solution

Given information:

The given function is $y=\sin 3x+\cos 4x,0\le x\le 2\pi$

Consider the given function.

Determine the second derivative and equate with zero.

  $\begin{array}{c}f\text{'}\text{'}\left(x\right)=-9\sin 3x-16\cos 4x\\ 0=-9\sin 3x-16\cos 4x\end{array}$

So, the points where double derivative is zero:

  $x\approx 0.542,x\approx 1.266,x\approx 1.876,x\approx 2.6,x\approx 3.425,x\approx 4.281,x=5.144,x\approx 6.0$

Now draw the table 2:

Intervals	$\left(0,0.542\right)$	$\left(0.542,1.266\right)$	$\left(1.266,1.876\right)$	$\left(1.876,2.6\right)$	$\left(2.6,3.425\right)$
Sign of derivative	$-$	$+$	$-$	$+$	$-$
Behavior of y	Concave down	Concave up	Concave down	Concave up	Concave down
Intervals	$\left(3.425,4.281\right)$	$\left(4.281,5.144\right)$	$\left(5.144,6\right)$	$\left(6,2\pi \right)$
Sign of derivative	$+$	$-$	$+$	$-$
Behavior of y	Concave up	Concave down	Concave up	Concave down

From the table 2 it can be observed that the function is concave up in the interval $\left(0.542,1.266\right)$ , $\left(1.876,2.6\right)$ , $\left(3.425,4.281\right)$ , $\left(5.144,6\right)$ .

d.

To determine

To identify: The interval in which the function $y=\sin 3x+\cos 4x,0\le x\le 2\pi$ is concave down.

Answer to Problem 12RE

The function is concave down in the interval $\left(0,0.542\right)$ , $\left(1.266,1.876\right)$ , $\left(2.6,3.425\right)$ , $\left(4.281,5.144\right)$ , $\left(6,2\pi \right)$ .

Explanation of Solution

Given information:

The given function is $y=\sin 3x+\cos 4x,0\le x\le 2\pi$

Consider the given function.

It is known that the table 2 is:

Intervals	$\left(0,0.542\right)$	$\left(0.542,1.266\right)$	$\left(1.266,1.876\right)$	$\left(1.876,2.6\right)$	$\left(2.6,3.425\right)$
Sign of derivative	$-$	$+$	$-$	$+$	$-$
Behavior of y	Concave down	Concave up	Concave down	Concave up	Concave down
Intervals	$\left(3.425,4.281\right)$	$\left(4.281,5.144\right)$	$\left(5.144,6\right)$	$\left(6,2\pi \right)$
Sign of derivative	$+$	$-$	$+$	$-$
Behavior of y	Concave up	Concave down	Concave up	Concave down

From the table 2 it can be observed that the function is concave down in the interval $\left(0,0.542\right)$ , $\left(1.266,1.876\right)$ , $\left(2.6,3.425\right)$ , $\left(4.281,5.144\right)$ , $\left(6,2\pi \right)$ .

Now draw the graph of the function.

  

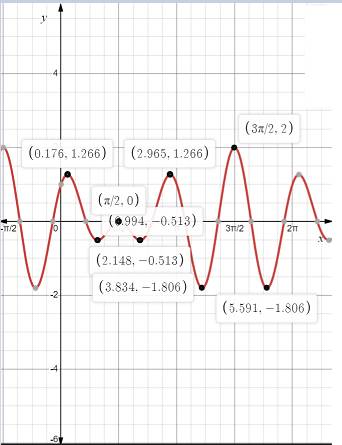
Thus, answer is verified from the graph.

e.

To determine

To identify: The local extreme values of the function $y=\sin 3x+\cos 4x,0\le x\le 2\pi$ .

Answer to Problem 12RE

The local extrema at $\left(3.834,-1.806\right),\left(\frac{3\pi }{2},2\right)\text{ and }\left(5.591,-1.806\right)$ are also extrema.

Explanation of Solution

Given information:

The given function is $y=\sin 3x+\cos 4x,0\le x\le 2\pi$

Consider the given function.

From the table 1 it can be observed that the function is concave down in the interval

(e) From the table (1) we have Local maxima at $\left(0.176,1.266\right),\left(\frac{\pi }{2},0\right),\left(2.965,1.266\right),\left(\frac{3\pi }{2},2\right)\text{ and }\left(2\pi ,1\right)$ . And Local minima at $\left(0,1\right),\left(0.994,-0.513\right),\left(2.148,-0.513\right),\left(3.834,-1.806\right)\text{ and }\left(5.591,-1.806\right).$

Note that the local extrema at $\left(3.834,-1.806\right),\left(\frac{3\pi }{2},2\right)\text{ and }\left(5.591,-1.806\right)$ are also extrema.

f.

To determine

To identify: The inflection points of the function $y=\sin 3x+\cos 4x,0\le x\le 2\pi$ .

Answer to Problem 12RE

The inflection points are: $\begin{array}{l}\left(0.542,0.437\right),\left(1.266,-0.267\right),\left(1.876,-0.267\right),\left(2.600,0.437\right),\left(3.425,-0.329\right),\\ \left(4.281,0.120\right),\left(5.144,0.120\right)\text{ and }\left(6.000,-0.329\right)\end{array}$

Explanation of Solution

Given information:

The given function is $y=\sin 3x+\cos 4x,0\le x\le 2\pi$

Consider the given function.

There are 8 inflection points given by $\begin{array}{l}\left(0.542,0.437\right),\left(1.266,-0.267\right),\left(1.876,-0.267\right),\left(2.600,0.437\right),\left(3.425,-0.329\right),\\ \left(4.281,0.120\right),\left(5.144,0.120\right)\text{ and }\left(6.000,-0.329\right)\end{array}$ .