Chapter 4, Problem 13RE

a.

To determine

To Find: The intervals on which the function is increasing using analytical method.

Answer to Problem 13RE

Function $y$ is increasing in the interval $\left(0,\frac{2}{\sqrt{3}}\right).$

Explanation of Solution

Given:

Function $y=\left\{\begin{array}{cc}{e}^{-x},& x\le 0\\ 4x-x^3,& x>0\end{array}\right\}$

Concept used:

If the derivative of a function is positive on an interval, then the function is increasing on that interval.

Also, if the derivative of a function is negative on an interval then the function is decreasing on that interval.

Calculation:

First derivative of $y$:

Differentiate the $y$ with respect to $x$ ,

  $\begin{array}{c}y=\left\{\begin{array}{cc}{e}^{-x},& x<0\\ 4x-x^3,& x>0\end{array}\right\}\\ \frac{d}{dx}\left(y\right)=\left\{\begin{array}{cc}\frac{d}{dx}\left(e^{-x}\right),& x<0\\ \frac{d}{dx}\left(4x-x^3\right),& x>0\end{array}\right\}\\ \frac{dy}{dx}=\left\{\begin{array}{cc}-e^{-x},& x<0\\ 4-3x^2,& x>0\end{array}\right\}\\ y\text{'}=\left\{\begin{array}{cc}-e^{-x},& x<0\\ 4-3x^2,& x>0\end{array}\right\}\end{array}$

Case 1: when $x<0$ then

  $y\text{'}=-e^{-x}$

Since, $-e^{-x}<0$ for all $x<0\text{ or }x\in (-\infty ,0)$ then $y\text{'}<0,\forall x\in (-\infty ,0)$ .

Hence, $y$ is not increasing in the interval $(-\infty ,0)$ .

Case 2:- when $x>0$ then

  $y\text{'}=4-3x^2$

According to a known result $y$ is increasing when $y\text{'}>0$ ,

  $\begin{array}{c}y\text{'}>0\\ 4-3x^2>0\\ 4>3x^2\\ 3x^2<4\\ x^2<\frac{4}{3}\\ x<\sqrt{\left(\frac{4}{3}\right)}\left(\because x>0\right)\\ x<\frac{2}{\sqrt{3}}\end{array}$

Thus, $0<x<\frac{2}{\sqrt{3}}.$

So, $y$ is increasing in the interval $\left(0,\frac{2}{\sqrt{3}}\right).$

Conclusion:

Function $y$ is increasing in the interval $\left(0,\frac{2}{\sqrt{3}}\right).$

b.

To determine

To Find: the intervals on which the function is decreasing using analytical method.

Answer to Problem 13RE

Function $y$ is decreasing in the interval $(-\infty ,0)$ and $\left(\frac{2}{\sqrt{3}},\infty \right).$

Explanation of Solution

Given:

Function $y=\left\{\begin{array}{cc}{e}^{-x},& x\le 0\\ 4x-x^3,& x>0\end{array}\right\}$

From part (a),

  $y\text{'}=\left\{\begin{array}{cc}-e^{-x},& x<0\\ 4-3x^2,& x>0\end{array}\right\}$

Concept used:

If the derivative of a function is positive on an interval, then the function is increasing on that interval.

Also, if the derivative of a function is negative on an interval then the function is decreasing on that interval.

Calculation:

First derivative of $y$ :

  $y\text{'}=\left\{\begin{array}{cc}-e^{-x},& x<0\\ 4-3x^2,& x>0\end{array}\right\}$

Case 1:- when $x\le 0$ then

  $y\text{'}=-e^{-x}$

Since, $-e^{-x}<0$ for all $x\le 0\text{ or }x\in (-\infty ,0)$ then $y\text{'}<0,\forall x\in (-\infty ,0)$ .

Hence, $y$ is decreasing in the interval $(-\infty ,0)$ .

Case 2:- when $x>0$ then

  $y\text{'}=4-3x^2$

According to result mentioned above $y$ is decreasing when $y\text{'}<0$ .

  $\begin{array}{c}y\text{'}<0\\ 4-3x^2<0\\ 4<3x^2\\ 3x^2>4\\ x^2>\frac{4}{3}\\ x>\sqrt{\left(\frac{4}{3}\right)}\left(\because x>0\right)\\ x>\frac{2}{\sqrt{3}}.\end{array}$

So, $y$ is decreasing in the interval $\left(\frac{2}{\sqrt{3}},\infty \right).$

Conclusion:

Function $y$ is decreasing in the interval $(-\infty ,0)$ and $\left(\frac{2}{\sqrt{3}},\infty \right).$

c.

To determine

Find the intervals on which the function is concave up using analytical method.

Answer to Problem 13RE

Function $y$ is concave up in the interval $(-\infty ,0)$ .

Explanation of Solution

Given:

Function $y=\left\{\begin{array}{cc}{e}^{-x},& x\le 0\\ 4x-x^3,& x>0\end{array}\right\}$

First derivative of $y$ :-

  $y\text{'}=\left\{\begin{array}{cc}-e^{-x},& x<0\\ 4-3x^2,& x>0\end{array}\right\}$

Concept used:

If the second derivative of a function is positive on an interval, then the function is concave up on that interval.

Also, if the second derivative of a function is negative on an interval then the function is concave down on that interval.

Calculation:

First derivative of $y$:

  $y\text{'}=\left\{\begin{array}{cc}-e^{-x},& x<0\\ 4-3x^2,& x>0\end{array}\right\}$

Second derivative of $y$:

Differentiate the $y\text{'}$ with respect to $x$ ,

  $\begin{array}{c}y\text{'}=\left\{\begin{array}{cc}-e^{-x},& x<0\\ 4-3x^2,& x>0\end{array}\right\}\\ \frac{d}{dx}\left(y\text{'}\right)=\left\{\begin{array}{cc}\frac{d}{dx}\left(-e^{-x}\right),& x<0\\ \frac{d}{dx}\left(4-3x^2\right),& x>0\end{array}\right\}\\ y\text{'}\text{'}=\left\{\begin{array}{cc}{e}^{-x},& x<0\\ -6x,& x>0\end{array}\right\}\end{array}$

Case 1: when $x<0$ then

  $y\text{'}\text{'}=e^{-x}$

Since, $e^{-x}>0\text{ for all }x\le 0\text{ or }x\in (-\infty ,0)\text{ then }y\text{'}\text{'}>0,\forall x\in (-\infty ,0).$

  $$

Hence, $y$ is concave up in the interval $(-\infty ,0)$ .

Case 2:- when $x>0$ then

  $y\text{'}\text{'}=-6x$

According to a known result $y$ is concave up when $y\text{'}\text{'}>0$ .

  $\begin{array}{c}y\text{'}\text{'}>0\\ -6x>0\\ x<0\text{ (but given that }x>0).\end{array}$

So, $y$ is not concave up when $x>0\text{ or }x\in \left(0,\infty \right).$

Conclusion:

Function $y$ is concave up in the interval $(-\infty ,0)$ .

d.

To determine

Find the intervals on which the function is concave down using analytical method.

Answer to Problem 13RE

Function $y$ is concave down in the interval $\left(0,\infty \right)$ .

Explanation of Solution

Given:

Function $y=\left\{\begin{array}{cc}{e}^{-x},& x\le 0\\ 4x-x^3,& x>0\end{array}\right\}$

First derivative of $y$ :

  $y\text{'}=\left\{\begin{array}{cc}-e^{-x},& x<0\\ 4-3x^2,& x>0\end{array}\right\}$

Second derivative of $y$ :

  $y\text{'}\text{'}=\left\{\begin{array}{cc}{e}^{-x},& x<0\\ -6x,& x>0\end{array}\right\}$

Concept used:

If the second derivative of a function is positive on an interval, then the function is concave up on that interval.

Also, if the second derivative of a function is negative on an interval, then the function is concave down on that interval.

Calculation:

Second derivative of $y$:

  $y\text{'}\text{'}=\left\{\begin{array}{cc}{e}^{-x},& x<0\\ -6x,& x>0\end{array}\right\}$

Case 1:- when $x<0$ then

  $y\text{'}\text{'}=e^{-x}$

Since, $e^{-x}>0$ for all $x\le 0\text{ or }x\in (-\infty ,0)$ then $y\text{'}\text{'}>0,\forall x\in (-\infty ,0)$ .

Hence, $y$ is not concave down in the interval $(-\infty ,0)$ .

Case 2:- when $x>0$ then

  $y\text{'}\text{'}=-6x$

According to a known result $y$ is concave down when $y\text{'}\text{'}<0$ .

  $\begin{array}{c}y\text{'}\text{'}<0\\ -6x<0\\ x>0.\end{array}$

So, $y$ is concave down when $x>0$ or $x\in \left(0,\infty \right)$ .

Graph of function $y$:

  

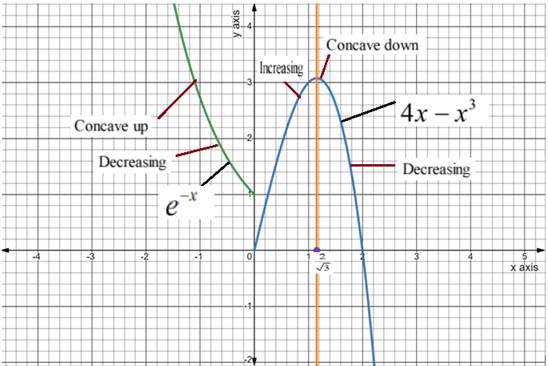
Conclusion:

Function $y$ is concave down in the interval $\left(0,\infty \right)$ .

e.

To determine

Find local extreme values using the graph.

Answer to Problem 13RE

Function has local maxima at $x=\frac{2}{\sqrt{3}}\text{ or }x=\frac{2\sqrt{3}}{3}$ .

Explanation of Solution

Given:

Function $y=\left\{\begin{array}{cc}{e}^{-x},& x\le 0\\ 4x-x^3,& x>0\end{array}\right\}$

Graph of function:

  

Calculation:

According to the graph,

Function has local maxima at $x=\frac{2}{\sqrt{3}}\text{ or }x=\frac{2\sqrt{3}}{3}$ .

Local minima do not exist for this function.

Conclusion:

Function has local maxima at $x=\frac{2}{\sqrt{3}}\text{ or }x=\frac{2\sqrt{3}}{3}$ .

f.

To determine

Find inflection points using the graph.

Answer to Problem 13RE

No inflection points.

Explanation of Solution

Given:

Function $y=\left\{\begin{array}{cc}{e}^{-x},& x\le 0\\ 4x-x^3,& x>0\end{array}\right\}$

Graph of function

  

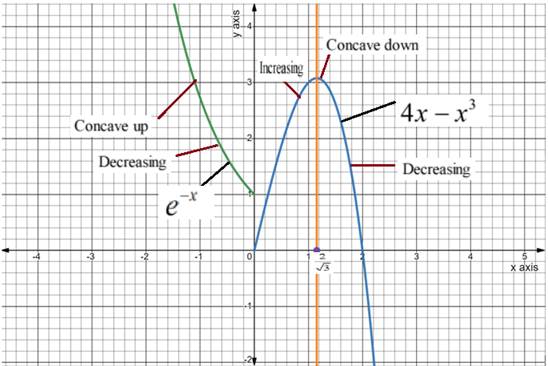
Concept used:

Inflection point: - A point of inflection on a curve is a continuous point at which the function changes its concavity.

Calculation:

According to the graph,

Function has jump discontinuity at $x=0$ .

But, according to the definition of inflection point function should be continuous at inflection point. So, the given function does not have inflection point.

Conclusion:

No inflection points.