Chapter 4.4, Problem 37E

a.

To determine

To find: To find the dimensions of the width and depth.

Answer to Problem 37E

The width are $4\sqrt{3}$ cm and depth is $4\sqrt{6}$ cm.

Explanation of Solution

Given:

The strength S of a rectangle wooden beam is proportional to its width times the square of its depth.

  $S=kw{d}^2$

Where S,w,d,k are the strength, width, depth and a constant respectively.

Concept Used: Pythagoras Thoerem.

Calculation:

Considering the figure, by Pythagoras theorem

The square of the hypotenuse is equal to the sum of square of adjacent side and opposite side.

  $\begin{array}{c}$ {(12)}^2=w^2+d^2$144=w^2+d^2\\ 144-w^2=d^2\\ d=\sqrt{144-w^2}\end{array}$

Substituting $144-w^2=d^2$ in the $S=kw{d}^2$

  $\begin{array}{l}S=(kw)(144-w^2)\\ S=144kw-k{w}^3\end{array}$

For any function $f(x)$ the condition of minimum and maximum is obtained by finding $f\text{'}(x)=0$ , critical points and end points

  $\begin{array}{l}\frac{dS}{dw}=\frac{d}{dw}(144kw-k{w}^3)\\ \frac{dS}{dw}=144k-3k{w}^2\end{array}$

Substituting $\frac{dS}{dw}=0$ in the above equation

  $\begin{array}{c}0=144k-3k{w}^2\\ 144k=3k{w}^2\\ 144=3w^2\\ \frac{144}{3}=w^2\\ w=\pm \sqrt{48}\end{array}$

Since $0<w<12$ and $k=1$ considering only $w=\sqrt{48}$ .

The critical points occurs at $w=\sqrt{48}$ .

  $\frac{dS}{dw}>0$ for $0<w<\sqrt{48}$ and $\frac{dS}{dw}<0$ for $\sqrt{48}<w<12$ .

  $\begin{array}{l}w=\sqrt{48}\\ w=4\sqrt{3}\\ d=\sqrt{144-w^2}\\ d=\sqrt{144-48}\\ d=\sqrt{96}\\ d=4\sqrt{6}\end{array}$

For maximum strength, the dimensions are width is $4\sqrt{3}$ cm, the depth is $4\sqrt{6}$ cm.

b.

To determine

To find: To find the dimensions of the width.

Answer to Problem 37E

The width are $4\sqrt{3}$ cm .

Explanation of Solution

Given:

The strength S of a rectangle wooden beam is proportional to its width times the square of its depth.

  $S=kw{d}^2$

Where S,w,d,k are the strength, width, depth and a constant respectively.

Calculation:

  

Plotting the graph between S and w

For maximum strength, the dimensions are width is $4\sqrt{3}=6.9$ cm.

It is same as obtained in a.

b.

To determine

To find: To find the dimensions of the depth.

Answer to Problem 37E

The depth is $4\sqrt{6}$ cm .

Explanation of Solution

Given:

The strength S of a rectangle wooden beam is proportional to its width times the square of its depth.

  $S=kw{d}^2$

Where S,w,d,k are the strength, width, depth and a constant respectively.

Calculation:

  

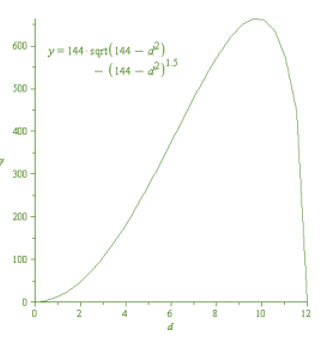
Plotting the graph between S and d.

For maximum strength, the dimensions are depth is $4\sqrt{6}=9.8$ cm.

It is same as obtained in a.

The change in the value of k, will change the maximum strength but it will not change the dimension of the strongest beam, since dimensions are independent of k. For different values of k, the graph will be same expect that the vertical scale will be different.