Chapter 4.4, Problem 57E

To determine

To prove : The angle of incidence is equal to the angle of reflection.

Explanation of Solution

Given information : The figure given is

  

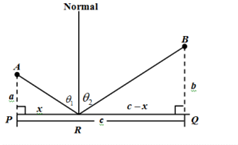
Formula used : Distance $D=\sqrt{{(x_1-x_2)}^2+{(y_1-y_2)}^2}$

Proof:

Considering the figure, here the point PA is the perpendicular on PQ from the point A. QB is another perpendicular on PQ from the point B. Light strikes the mirror at the point R.

Here

a= the distance from A to P.

b= the distance from B to Q.

c= the distance from P to Q.

x= the distance from P to R.

For the light the distance from A to B is

  $D(x)=\sqrt{x^2+a^2}+\sqrt{{(c-x)}^2+b^2}$

The derivative of the distance is

  $\begin{array}{l}D\text{'}(x)=\frac{2x}{2\sqrt{x^2+a^2}}+\frac{-2(c-x)}{2\sqrt{{(c-x)}^2+b^2}}\\ D\text{'}(x)=\frac{x}{\sqrt{x^2+a^2}}-\frac{(c-x)}{\sqrt{{(c-x)}^2+b^2}}\end{array}$

For any function $f(x)$ the condition of minimum and maximum is obtained by finding $f\text{'}(x)=0$ , critical points and end points

  $\begin{array}{l}D\text{'}(x)=\frac{x}{\sqrt{x^2+a^2}}-\frac{(c-x)}{\sqrt{{(c-x)}^2+b^2}}\\ 0=\frac{x}{\sqrt{x^2+a^2}}-\frac{(c-x)}{\sqrt{{(c-x)}^2+b^2}}\\ \frac{x}{\sqrt{x^2+a^2}}=\frac{(c-x)}{\sqrt{{(c-x)}^2+b^2}}\end{array}$

Squaring of both sides

  $\begin{array}{l}{\left(\frac{x}{\sqrt{x^2+a^2}}\right)}^2={\left(\frac{(c-x)}{\sqrt{{(c-x)}^2+b^2}}\right)}^2\\ \frac{x^2}{x^2+a^2}=\frac{{(c-x)}^2}{{(c-x)}^2+b^2}\\ x^2\left({(c-x)}^2+b^2\right)={(}^c\left(x^2+a^2\right)\\ x^2(c^2+x^2-2cx+b^2)=(c^2+x^2-2cx+b^2)(x^2+a^2)\\ $ x^2{b}^2=a^2{(c-x)}^2$\end{array}$

  $\begin{array}{l}{x}^2{b}^2=a^2(c^2+x^2-2cx)\\ x=\frac{ac}{(a+b)},\frac{ac}{(a-b)}\end{array}$

Here $x=\frac{ac}{(a-b)}$ is an extraneous solution, consider only $x=\frac{ac}{(a+b)}$ .

Critical point occurs at $x=\frac{ac}{(a+b)}$

D is differentiable for all values value of x in the domain $[0,c]$

  $\begin{array}{l}\frac{dD(0)}{dx}=\frac{-c}{\sqrt{c^2-b^2}}<0\\ \frac{dD(c)}{dx}=\frac{-c}{\sqrt{c^2-b^2}}>0\end{array}$

It shows D is decreasing from $x=0$ to $x=c$ .It gives $x=\frac{ac}{(a+b)}$ corresponding to minimum

  $\frac{PR}{AR}=\frac{QR}{BR}$

And right triangles APR and BQR are similar which in turn gives two angles,

  ${\theta }_1={\theta }_2$

Hence proved angle of incidence is equal to the angle of reflection.