Chapter 4, Problem 15RE

a.

To determine

To Find: the intervals on which the function is increasing using analytical method.

Answer to Problem 15RE

Function $y$ is increasing in the interval $\left(0,\frac{8}{9}\right)$ .

Explanation of Solution

Given:

Function $y=x^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\left(2-x\right)$

Concept used:

If the derivative of a function is positive on an interval, then the function is increasing on that interval.

Also, if the derivative of a function is negative on an interval then the function is decreasing on that interval.

Calculation:

Rewrite the function,

  $\begin{array}{l}y=x^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\left(2-x\right)\\ =2x^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-x^{\raisebox{1ex}{$9$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\end{array}$

First derivative of $y$:

Differentiate the $y$ with respect to $x$ ,

  $\begin{array}{c}y=2x^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-x^{\raisebox{1ex}{$9$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ \\ \frac{d}{dx}\left(y\right)=\frac{d}{dx}\left(2x^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-x^{\raisebox{1ex}{$9$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\right)\\ y\text{'}=\frac{8}{5}{x}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-\frac{9}{5}{x}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ y\text{'}=\frac{8}{5x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}}-\frac{9}{5}{x}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\end{array}$

According to a known result $y$ is increasing when $y\text{'}>0$ .

  $\begin{array}{c}y\text{'}>0\\ \frac{8}{5x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}}-\frac{9}{5}{x}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}>0\\ \frac{8}{5x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}}>\frac{9}{5}{x}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ \frac{8}{9}>x^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}{x}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ \frac{8}{9}>x\left(\because x^{\frac{4}{5}+\frac{1}{5}}=x^{\frac{5}{5}}=x\right)\\ x<\frac{8}{9}\end{array}$

Case 1:- when $x<0$ , then

  $\begin{array}{c}\text{Take }x={\left(-2\right)}^5\\ y\text{'}=\frac{8}{5x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}}-\frac{9}{5}{x}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ \text{Put }x={\left(-2\right)}^5\\ y\text{'}=\frac{8}{5{\left({\left(-2\right)}^5\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}}-\frac{9}{5}{\left({\left(-2\right)}^5\right)}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ =\frac{8}{5\left(-2\right)}-\frac{9}{5}{\left(-2\right)}^4\\ =\frac{-4}{5}-\frac{144}{5}=-\frac{148}{5}\\ =-\frac{148}{5}<0\end{array}$

So, $y$ is increasing in the interval $\left(0,\frac{8}{9}\right)$ .

Conclusion:

Function $y$ is increasing in the interval $\left(0,\frac{8}{9}\right)$ .

b.

To determine

To Find the intervals on which the function is decreasing using analytical method.

Answer to Problem 15RE

Function $y$ is decreasing in the interval $\left(-\infty ,0\right)\text{ and }\left(\frac{8}{9},\infty \right).$

Explanation of Solution

Given:

Function $y=2x^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-x^{\raisebox{1ex}{$9$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$

From part (a), first derivative of $y$

  $y\text{'}=\frac{8}{5x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}}-\frac{9}{5}{x}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$

Concept used:

If the derivative of a function is positive on an interval, then the function is increasing on that interval.

Also, if the derivative of a function is negative on an interval then the function is decreasing on that interval.

Calculation:

First derivative of $y$:-

  $y\text{'}=\frac{8}{5x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}}-\frac{9}{5}{x}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$

According to a known result $y$ is decreasing when $y\text{'}<0$ .

  $\begin{array}{c}y\text{'}<0\\ \frac{8}{5x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}}-\frac{9}{5}{x}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}<0\\ \frac{8}{5x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}}<\frac{9}{5}{x}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ \frac{8}{9}<x^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}{x}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ \frac{8}{9}<x\left(\because x^{\frac{4}{5}+\frac{1}{5}}=x^{\frac{5}{5}}=x\right)\\ x>\frac{8}{9}\\ x\in \left(\frac{8}{9},\infty \right)\end{array}$

Also, from part (a): $y\text{'}<0$ when $x<0$ .

So, $y$ is decreasing in the interval $\left(-\infty ,0\right)\text{ and }\left(\frac{8}{9},\infty \right)$ .

Conclusion:

Function $y$ is decreasing in the interval $\left(-\infty ,0\right)\text{ and }\left(\frac{8}{9},\infty \right)$ .

c.

To determine

Find the intervals on which the function is concave up using analytical method.

Answer to Problem 15RE

Function $y$ is concave up in the interval $\left(-\infty ,\frac{-2}{9}\right).$ .

Explanation of Solution

Given:

Function $y=2x^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-x^{\raisebox{1ex}{$9$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$

First derivative of $y$ :-

  $y\text{'}=\frac{8}{5x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}}-\frac{9}{5}{x}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$

Concept used:

If the second derivative of a function is positive on an interval, then the function is concave up on that interval.

Also, if the second derivative of a function is negative on an interval then the function is concave down on that interval.

Calculation:

First derivative of $y$ :

  $y\text{'}=\frac{8}{5x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}}-\frac{9}{5}{x}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$

Second derivative of $y$ :

Differentiate the $y\text{'}$ with respect to $x$ ,

  $\begin{array}{c}y\text{'}=\frac{8}{5x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}}-\frac{9}{5}{x}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ \frac{d}{dx}\left(y\text{'}\right)=\frac{d}{dx}\left(\frac{8}{5}{x}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-\frac{9}{5}{x}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\right)\\ y\text{'}\text{'}=\left(\frac{8}{5}\left(\frac{-1}{5}\right)x^{\raisebox{1ex}{$-6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-\frac{9}{5}\left(\frac{4}{5}\right)x^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\right)\\ y\text{'}\text{'}=-\frac{8}{25}{x}^{\raisebox{1ex}{$-6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-\frac{36}{25}{x}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\end{array}$

According to a known result $y$ is concave up when $y\text{'}\text{'}>0$ .

  $\begin{array}{c}y\text{'}\text{'}>0\\ -\frac{8}{25}{x}^{\raisebox{1ex}{$-6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-\frac{36}{25}{x}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}>0\\ -\frac{8}{25}{x}^{\raisebox{1ex}{$-6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}>\frac{36}{25}{x}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ -\frac{8}{25}{x}^{\raisebox{1ex}{$-6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}>\frac{36}{25}{x}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ -\frac{8}{36}>x^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}{x}^{\raisebox{1ex}{$6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ -\frac{2}{9}>x\left(\because x^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}{x}^{\raisebox{1ex}{$6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}=x^{\frac{-1}{5}+\frac{6}{5}}=x^{\frac{-1+6}{5}}=x^{\frac{5}{5}}=x\right)\\ x<-\frac{2}{9}\end{array}$

So, $y$ is concave up in the interval $\left(-\infty ,\frac{-2}{9}\right).$

Conclusion:

Function $y$ is concave up in the interval $\left(-\infty ,\frac{-2}{9}\right).$

d.

To determine

Find the intervals on which the function is concave down using analytical method.

Answer to Problem 15RE

Function $y$ is concave down in the interval $\left(\frac{-2}{9},\text{ 0}\right)\text{ and }\left(0,\infty \right).$ .

Explanation of Solution

Given:

Function $y=2x^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-x^{\raisebox{1ex}{$9$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$

First derivative of $y$ :

  $y\text{'}=\frac{8}{5x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}}-\frac{9}{5}{x}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$

Second derivative of $y$ :

  $y\text{'}\text{'}=-\frac{8}{25}{x}^{\raisebox{1ex}{$-6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-\frac{36}{25}{x}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$

Concept used:

If the second derivative of a function is positive on an interval, then the function is concave up on that interval.

Also, if the second derivative of a function is negative on an interval then the function is concave down on that interval.

Calculation:

Second derivative of $y$ :

  $y\text{'}\text{'}=-\frac{8}{25}{x}^{\raisebox{1ex}{$-6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-\frac{36}{25}{x}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$

According to a known result $y$ is concave down when $y\text{'}\text{'}<0$ .

  $\begin{array}{c}y\text{'}\text{'}<0\\ -\frac{8}{25}{x}^{\raisebox{1ex}{$-6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-\frac{36}{25}{x}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}<0\\ -\frac{8}{25}{x}^{\raisebox{1ex}{$-6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}<\frac{36}{25}{x}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ -\frac{8}{25}{x}^{\raisebox{1ex}{$-6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}<\frac{36}{25}{x}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ -\frac{8}{36}<x^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}{x}^{\raisebox{1ex}{$6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}\\ -\frac{2}{9}<x\left(\because x^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}{x}^{\raisebox{1ex}{$6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}=x^{\frac{-1}{5}+\frac{6}{5}}=x^{\frac{-1+6}{5}}=x^{\frac{5}{5}}=x\right)\\ x>-\frac{2}{9}\end{array}$

So, $y$ is concave down in the interval $\left(\frac{-2}{9},\text{ 0}\right)\text{ and }\left(0,\infty \right).$

Graph of function$y$

:

  

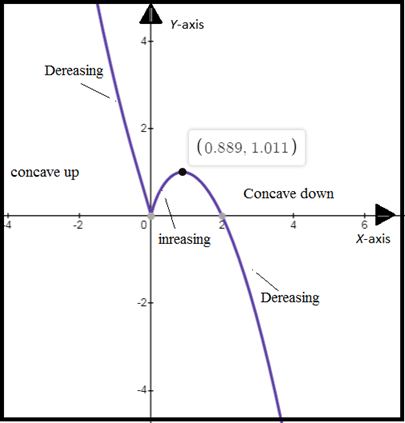
Conclusion:

Function $y$ is concave down in the interval $\left(\frac{-2}{9},\text{ 0}\right)\text{ and }\left(0,\infty \right).$

e.

To determine

Find the local extreme values using the graph.

Answer to Problem 15RE

Function has local maxima at $x=\frac{8}{9}\approx 0.889$ .

Function has local minima at $x=0$ .

Explanation of Solution

Given:

Function $y=2x^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-x^{\raisebox{1ex}{$9$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$

Graph of function

  

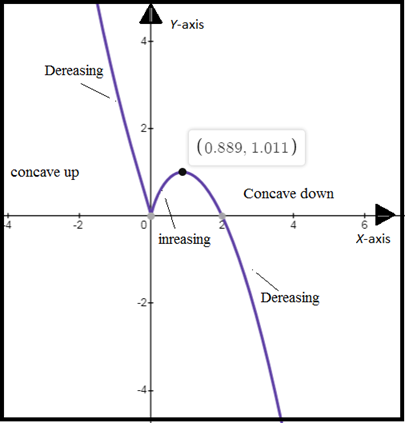
Calculation:

According to the graph,

Function has local maxima at $x=\frac{8}{9}\approx 0.889$ .

Function has local minima at $x=0$ .

Conclusion:

Function has local maxima at $x=\frac{8}{9}\approx 0.889$ .

Function has local minima at $x=0$ .

f.

To determine

Find inflection points using the graph.

Answer to Problem 15RE

Inflection point $x=\frac{-2}{9}$ .

Explanation of Solution

Given:

Function $y=2x^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-x^{\raisebox{1ex}{$9$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$

Second derivative of $y$ :

  $y\text{'}\text{'}=-\frac{8}{25}{x}^{\raisebox{1ex}{$-6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-\frac{36}{25}{x}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$

Concept used:

Inflection point: A point of inflection on a curve is a continuous point at which the function changes its concavity.

Calculation:

Second derivative of $y$ :

  $y\text{'}\text{'}=-\frac{8}{25}{x}^{\raisebox{1ex}{$-6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-\frac{36}{25}{x}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$

For inflection point put $y\text{'}\text{'}=0$ ,

  $\begin{array}{c}y\text{'}\text{'}=0\\ -\frac{8}{25}{x}^{\raisebox{1ex}{$-6$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}-\frac{36}{25}{x}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}=0\\ x=-\frac{2}{9}\end{array}$

Inflection point $x=\frac{-2}{9}$ .

Conclusion:

Inflection point $x=\frac{-2}{9}$ .