
a.
To identify: The interval in which the function
a.
Answer to Problem 16RE
The function is increasing in the interval
Explanation of Solution
Given information:
The given function is
Consider the given function.
Calculate the derivative of the function.
Now determine the critical points.
By putting
So, the critical points are: 2 and 0.215.
The required intervals are:
Now draw the table 1:
| Intervals | |||
| Sign of derivative | |||
| Behavior of y | Increasing | Decreasing | Decreasing |
Thus, from the table 1 it can be observed that the function is increasing in the interval
b.
To identify: The interval in which the function
b.
Answer to Problem 16RE
The function is decreasing in the interval
Explanation of Solution
Given information:
The given function is
It is known that the table 1 is:
| Intervals | |||
| Sign of derivative | |||
| Behavior of y | Increasing | Decreasing | Decreasing |
Thus, from the table 1 it can be observed that the function is decreasing in the interval
c.
To identify: The interval in which the function
c.
Answer to Problem 16RE
The function is concave up in the interval
Explanation of Solution
Given information:
The given function is
Consider the given function.
Determine the second derivative and equate with zero.
So, the points where double derivative is zero
Also, function is not defined at
Now draw the table 2:
| Intervals | |||
| Sign of derivative | |||
| Behavior of y | Concave down | Concave up | Concave down |
From the table 2 it can be observed that the function is concave up in the interval
d.
To identify: The interval in which the function
d.
Answer to Problem 16RE
The function is concave down in the interval
Explanation of Solution
Given information:
The given function is
Consider the given function.
It is known that the table 2 is:
| Intervals | |||
| Sign of derivative | |||
| Behavior of y | Concave down | Concave up | Concave down |
From the table 2 it can be observed that the function is concave down in the interval
Now draw the graph of the function.
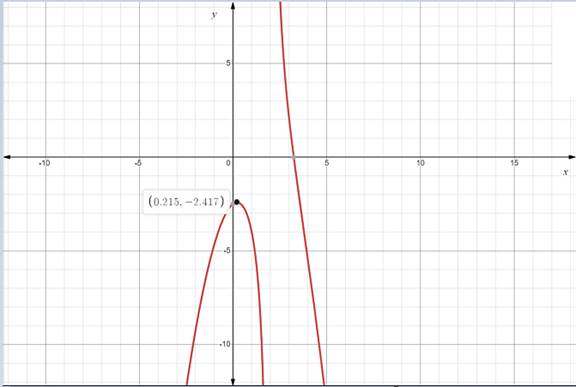
Thus, answer is verified from the graph.
e.
To identify: The local extreme values of the function
e.
Answer to Problem 16RE
Explanation of Solution
Given information:
The given function is
Consider the given function.
The value of y at these critical points
At
Thus, local
f.
To identify: The inflection points of the function
f.
Answer to Problem 16RE
The inflection point is:
Explanation of Solution
Given information:
The given function is
Consider the given function.
From the table it can be observed that there is only one inflation point which is:
Chapter 4 Solutions
Advanced Placement Calculus Graphical Numerical Algebraic Sixth Edition High School Binding Copyright 2020
- 3) If a is a positive number, what is the value of the following double integral? 2a Love Lv 2ay-y² .x2 + y2 dadyarrow_forward16. Solve each of the following equations for x. (a) 42x+1 = 64 (b) 27-3815 (c) 92. 27² = 3-1 (d) log x + log(x - 21) = 2 (e) 3 = 14 (f) 2x+1 = 51-2xarrow_forward11. Find the composition fog and gof for the following functions. 2 (a) f(x) = 2x+5, g(x) = x² 2 (b) f(x) = x²+x, g(x) = √√x 1 (c) f(x) = -1/2) 9 9(x) = х = - Xarrow_forward
- practice problem please help!arrow_forward13. A restaurant will serve a banquet at a cost of $20 per person for the first 50 people and $15 for person for each additional person. (a) Find a function C giving the cost of the banquet depending on the number of people p attending. (b) How many people can attend the banquet for $2000?arrow_forwardAlt Fn Ctrl 12. Find functions f and g such that h(x) = (fog)(x). (a) h(x) = (x² + 2)² x+1 (b) h(x) = 5 3arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





