Chapter 4, Problem 14RE

a.

To determine

Find the intervals on which the function is increasing using analytical method.

Answer to Problem 14RE

Function $y$ is increasing in the interval $\left(-0.57809,1.69168\right).$

Explanation of Solution

Given:

Function $y=-x^5+\frac{7}{3}{x}^3+5x^2+4x+2$

Concept used:

If the derivative of a function is positive on an interval, then the function is increasing on that interval.

Also, if the derivative of a function is negative on an interval, then the function is decreasing on that interval.

Calculation:

First derivative of $y$:- Differentiate the $y$ with respect to $x$ ,

  $\begin{array}{c}y=-x^5+\frac{7}{3}{x}^3+5x^2+4x+2\\ \frac{d}{dx}\left(y\right)=\frac{d}{dx}\left(-x^5+\frac{7}{3}{x}^3+5x^2+4x+2\right)\\ y\text{'}=-5x^4+\frac{7}{3}\left(3x^2\right)+5\left(2x\right)+4\\ y\text{'}=-5x^4+7x^2+10x+4\end{array}$

For solution put $y\text{'}=0$ ,

  $\begin{array}{c}y\text{'}=0\\ -5x^4+7x^2+10x+4=0.\end{array}$

Thus, $x=-0.57809,1.69168$ .

According to a known result $y$ is increasing when $y\text{'}>0$ .

  $\begin{array}{c}y\text{'}>0\\ -5x^4+7x^2+10x+4>0\\ x>-0.57809\text{ and }x>\mathrm{1.69168.}\end{array}$

Thus, $x\in \left(-0.57809,1.69168\right)$ .

So, $y$ is increasing in the interval $\left(-0.57809,1.69168\right).$

Conclusion:

Function $y$ is increasing in the interval $\left(-0.57809,1.69168\right).$

b.

To determine

Find the intervals on which the function is decreasing using analytical method.

Answer to Problem 14RE

Function $y$ is decreasing in the interval $\left(-\infty ,-0.57809\right)\text{ and }\left(1.69168,\infty \right).$

Explanation of Solution

Given:

Function $y=-x^5+\frac{7}{3}{x}^3+5x^2+4x+2$

From part (a), first derivative of $y$

  $y\text{'}=-5x^4+7x^2+10x+4$

Concept used:

If the derivative of a function is positive on an interval, then the function is increasing on that interval.

Also, if the derivative of a function is negative on an interval, then the function is decreasing on that interval.

Calculation:

First derivative of $y$:-

  $y\text{'}=-5x^4+7x^2+10x+4$

According to a known result $y$ is decreasing when $y\text{'}<0$ ,

  $\begin{array}{c}y\text{'}<0\\ -5x^4+7x^2+10x+4<0\\ x<-0.57809\text{ and }x<1.69168,\end{array}$

Thus, $x\in \left(-\infty ,-0.57809\right)\text{ and }x\in \left(1.69168,\infty \right)$ .

So, $y$ is decreasing in the interval $\left(-\infty ,-0.57809\right)\text{ and }\left(1.69168,\infty \right).$

Conclusion:

Function $y$ is decreasing in the interval $\left(-\infty ,-0.57809\right)\text{ and }\left(1.69168,\infty \right).$

c.

To determine

Find the intervals on which the function is concave up using analytical method.

Answer to Problem 14RE

Function $y$ is concave up in the interval $\left(-\infty ,1.07867\right).$ .

Explanation of Solution

Given:

Function $y=-x^5+\frac{7}{3}{x}^3+5x^2+4x+2$

First derivative of $y$:-

  $y\text{'}=-5x^4+7x^2+10x+4$

Concept used:

If the second derivative of a function is positive on an interval, then the function is concave up on that interval.

Also, if the second derivative of a function is negative on an interval, then the function is concave down on that interval.

Calculation:

First derivative of $y$:

  $y\text{'}=-5x^4+7x^2+10x+4$

Second derivative of $y$:

Differentiate the $y\text{'}$ with respect to $x$ ,

  $\begin{array}{c}y\text{'}=-5x^4+7x^2+10x+4\\ \frac{d}{dx}\left(y\text{'}\right)=\frac{d}{dx}\left(-5x^4+7x^2+10x+4\right)\\ y\text{'}\text{'}=-20x^3+14x+10\end{array}$

For solution put $y\text{'}\text{'}=0$ ,

  $\begin{array}{c}y\text{'}\text{'}=0\\ -20x^3+14x+10=0\\ x=1.07867\end{array}$

Since, $-20x^3+14x+10$ is an odd degree polynomial with negative leading coefficient. So, graph will increase in left and falls in right then $y\text{'}\text{'}=-20x^3+14x+10>0\text{ when }x<1.07867\text{ and }y\text{'}\text{'}=-20x^3+14x+10<0\text{ when }x>\mathrm{1.07867.}$

According to a known result $y$ is concave up when $y\text{'}\text{'}>0$ ,

  $\begin{array}{c}y\text{'}\text{'}>0\\ -20x^3+14x+10>0\\ x<1.07867\end{array}$

Thus, $x\in \left(-\infty ,1.07867\right)$ .

So, $y$ is concave up in the interval $\left(-\infty ,1.07867\right).$

Conclusion:

Function $y$ is concave up in the interval $\left(-\infty ,1.07867\right).$

d.

To determine

To Find: the intervals on which the function is concave down using analytical method.

Answer to Problem 14RE

Function $y$ is concave down in the interval $\left(1.07867,\infty \right).$

Explanation of Solution

Given:

Function $y=-x^5+\frac{7}{3}{x}^3+5x^2+4x+2$

First derivative of $y$ :

  $y\text{'}=-5x^4+7x^2+10x+4$

Second derivative of $y$ :

  $y\text{'}\text{'}=-20x^3+14x+10$

Concept used:

If the second derivative of a function is positive on an interval, then the function is concave up on that interval.

Also, if the second derivative of a function is negative on an interval then the function is concave down on that interval.

Calculation:

Second derivative of $y$ :

  $y\text{'}\text{'}=-20x^3+14x+10$

For solution put $y\text{'}\text{'}=0$ ,

  $\begin{array}{c}y\text{'}\text{'}=0\\ -20x^3+14x+10=0\\ x=1.07867\end{array}$

Since, $-20x^3+14x+10$ is an odd degree polynomial with negative leading coefficient. So, graph will increase in left and falls in right then $y\text{'}\text{'}=-20x^3+14x+10>0\text{ when }x<1.07867\text{ and }y\text{'}\text{'}=-20x^3+14x+10<0\text{ when }x>\mathrm{1.07867.}$

According to a known result $y$ is concave down when $y\text{'}\text{'}<0$ ,

  $\begin{array}{c}y\text{'}\text{'}<0\\ -20x^3+14x+10<0\\ x>1.07867\end{array}$

Thus, $x\in \left(1.07867,\infty \right)$ .

So, $y$ is concave down in the interval $\left(1.07867,\infty \right)$ .

Graph of function$y$

:

  

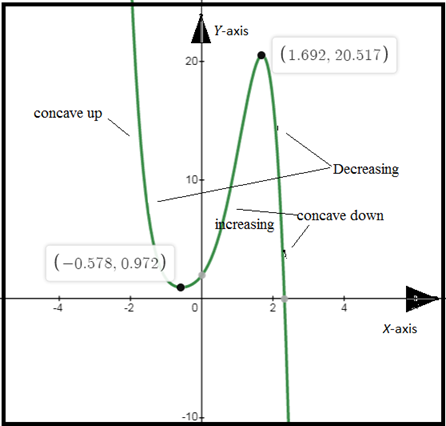
Conclusion:

Function $y$ is concave down in the interval $\left(1.07867,\infty \right)$ .

e.

To determine

Find local extreme values using the graph.

Answer to Problem 14RE

Function has local maxima at $x=1.692$ .

Function has local minima at $x=-0.578$ .

Explanation of Solution

Given:

Function $y=-x^5+\frac{7}{3}{x}^3+5x^2+4x+2$

Graph of function

  

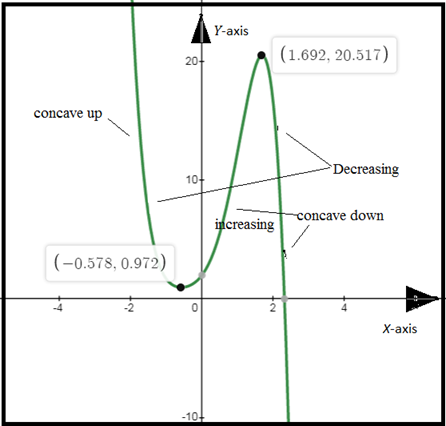
Calculation:

According to the graph,

Function has local maxima at $x=1.692$ .

Function has local minima at $x=-0.578$ .

Conclusion:

Function has local maxima at $x=1.692$ .

Function has local minima at $x=-0.578$ .

f.

To determine

Find inflection points using the graph.

Answer to Problem 14RE

Inflection point $x=1.07867$ .

Explanation of Solution

Given:

Function $y=-x^5+\frac{7}{3}{x}^3+5x^2+4x+2$

Second derivative of $y$ :

  $y\text{'}\text{'}=-20x^3+14x+10$

Concept used:

Inflection point: A point of inflection on a curve is a continuous point at which the function changes its concavity.

Calculation:

Second derivative of $y$ :

  $y\text{'}\text{'}=-20x^3+14x+10$

For inflection point put $y\text{'}\text{'}=0$ ,

  $\begin{array}{c}y\text{'}\text{'}=0\\ -20x^3+14x+10=0\\ x=\mathrm{1.07867.}\end{array}$

Inflection point: $x=1.07867$ .

Conclusion:

Inflection point is $x=1.07867$ .