
a.
Find the values at which the absolute maximum of
a.
Answer to Problem 28E
The absolute
Explanation of Solution
Given:
The function
Concept Used:
Calculation:
Function:
Differentiate the
For absolute maxima put
So, absolute maxima of function
Conclusion:
The absolute maxima of function
b.
Complete the table.
b.
Answer to Problem 28E
| 0.1 | 3.7150 | |
| 0.2 | 2.8650 | 0.4356 |
| 0.3 | 2.3646 | 0.4589 |
| 0.4 | 2.0188 | 0.4341 |
| 0.5 | 1.7564 | 0.3809 |
| 0.6 | 1.5474 | 0.3118 |
| 0.7 | 1.3755 | 0.2346 |
| 0.8 | 1.2308 | 0.1549 |
| 0.9 | 1.1071 | 0.0757 |
| 1 | 1 | 0 |
Explanation of Solution
Given:
The function
Graph of function
Calculation:
According to graph,
Then,
So, the graph is
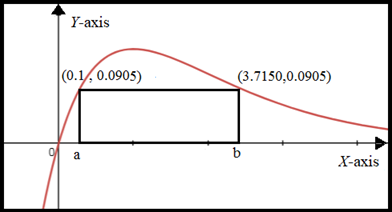
Area of rectangle
Area of rectangle is
Similarly, find the other values. The table is
| 0.1 | 3.7150 | |
| 0.2 | 2.8650 | 0.4356 |
| 0.3 | 2.3646 | 0.4589 |
| 0.4 | 2.0188 | 0.4341 |
| 0.5 | 1.7564 | 0.3809 |
| 0.6 | 1.5474 | 0.3118 |
| 0.7 | 1.3755 | 0.2346 |
| 0.8 | 1.2308 | 0.1549 |
| 0.9 | 1.1071 | 0.0757 |
| 1 | 1 | 0 |
c.
To Draw: a
c.
Answer to Problem 28E
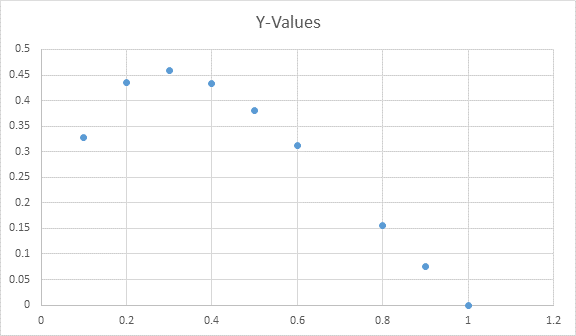
Explanation of Solution
Given:
| 0.1 | 3.7150 | |
| 0.2 | 2.8650 | 0.4356 |
| 0.3 | 2.3646 | 0.4589 |
| 0.4 | 2.0188 | 0.4341 |
| 0.5 | 1.7564 | 0.3809 |
| 0.6 | 1.5474 | 0.3118 |
| 0.7 | 1.3755 | 0.2346 |
| 0.8 | 1.2308 | 0.1549 |
| 0.9 | 1.1071 | 0.0757 |
| 1 | 1 | 0 |
Calculation:
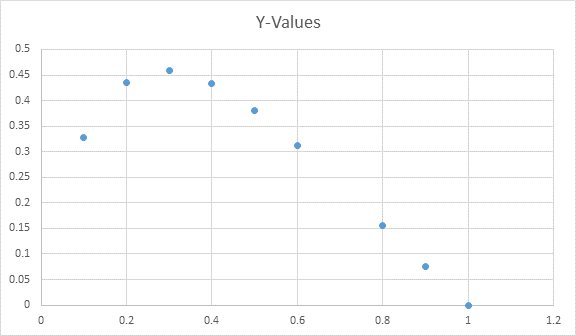
Here,
d.
To Find the quadratic, cubic and quartic regression equations for the data in part (b).
d.
Answer to Problem 28E
The absolute maxima of function
Explanation of Solution
Given:
The table is
| 0.1 | |
| 0.2 | 0.4356 |
| 0.3 | 0.4589 |
| 0.4 | 0.4341 |
| 0.5 | 0.3809 |
| 0.6 | 0.3118 |
| 0.7 | 0.2346 |
| 0.8 | 0.1549 |
| 0.9 | 0.0757 |
| 1 | 0 |
Concept used:
Here,
Calculation:
Quadratic regression equation:-
Here,
On solving,
Similarly, find the cubic and quartic regression equations.
Cubic regression equations
Quartic regression equations
Conclusion:
Quadratic regression equation
Cubic regression equations
Quartic regression equations
d.
Find maximum possible value of the area using the regression equations.
d.
Answer to Problem 28E
From quadratic regression equation,
Maximum possible area of the rectangle is
From cubic regression equation,
Maximum possible area of the rectangle is
From quartic regression equation,
Maximum possible area of the rectangle is
Explanation of Solution
Given:
Quadratic regression equation
Cubic regression equations
Quartic regression equations
Calculation:
Draw the graphs of regression equations,
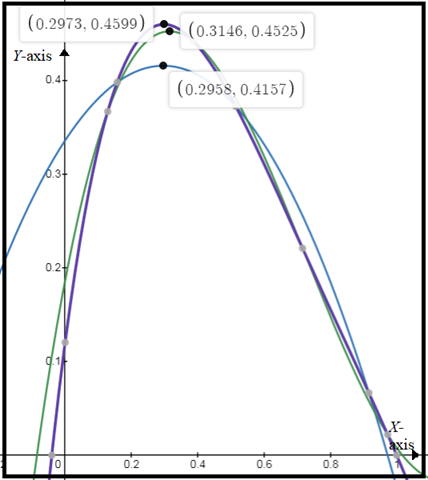
Now, according to graph,
From quadratic regression equation,
Maximum possible area of the rectangle is
From cubic regression equation,
Maximum possible area of the rectangle is
From quartic regression equation,
Maximum possible area of the rectangle is
Conclusion:
For quadratic regression equation:
For cubic regression equation:
For quartic regression equation:
Chapter 4 Solutions
Advanced Placement Calculus Graphical Numerical Algebraic Sixth Edition High School Binding Copyright 2020
- Good Day, Kindly assist me with the following query. Any assistance would be appreciated.arrow_forwardCan u give rough map of any room u can choose cm on toparrow_forward3. We'd like to know the first time when the population reaches 7000 people. First, graph the function from part (a) on your calculator or Desmos. In the same window, graph the line y = 7000. Notice that you will need to adjust your window so that you can see values as big as 7000! Investigate the intersection of the two graphs. (This video shows you how to find the intersection on your calculator, or in Desmos just hover the cursor over the point.) At what value t> 0 does the line intersect with your exponential function? Round your answer to two decimal places. (You don't need to show work for this part.) (2 points)arrow_forward
- Suppose the planet of Tattooine currently has a population of 6500 people and an annual growth rate of 0.35%. Use this information for all the problems below. 1. Find an exponential function f(t) that gives the population of Tattooine t years from now. (3 points)arrow_forwardA house was valued at $95,000 in the year 1988. The value appreciated to $170,000 by the year 2007. A) If the value is growing exponentially, what was the annual growth rate between 1988 and 2007? Round the growth rate to 4 decimal places. r = B) What is the correct answer to part A written in percentage form? r = 3 %.arrow_forwardB G R + K Match each equation with a graph above - 3(0.9)* 1 a. green (G) 3(1.5)* b. black (K) 3(0.73)* c. blue (B) d. red (R) I ✪ 4(1.21)* - 3(1.21)* e. orange (O)arrow_forward
- Suppose the planet of Tattooine currently has a population of 6500 people and an annual growth rate of 0.35%. Use this information for all the problems below.arrow_forwardTwo cables tied together at C are loaded as shown. Given: Q = 130 lb. 8 30° C B Q 3 4 Draw the free-body diagram needed to determine the range of values of P for which both cables remain taut.arrow_forwardCable AB is 103 ft long and the tension in the cable is 3900 lb. 56 ft A 50° 20° B x C Identify the angles 0.0, and 8, that define the direction of force. 1 By N 2 Match each of the options above to the items below. 142.1° 57.1° 73.3° 3 8.arrow_forward
- In the given figure, P = 51 lb . 65° C 25° 35° 75 lb P Determine the corresponding magnitude of the resultant. The corresponding magnitude of the resultant is| lb.arrow_forwardCable AB is 103 ft long and the tension in the cable is 3900 lb. 56 ft D y A B 20° 50° x C Identify the x, y, and z components of the force exerted by the cable on the anchor B. 1 F. FI 3 Fy 2 Match each of the options above to the items below. 2,120 lb 1,120 lb -3,076 lbarrow_forwardIn the given figure, P = 51 lb. 65° 25° 35° 75 lb P B Determine the required tension in cable AC, knowing that the resultant of the three forces exerted at point C of boom BC must be directed along BC. The required tension in cable AC is lb.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





