Chapter 4.1, Problem 9E

To determine

To Find: the absolute extreme value of the given graph, also, explain according to Extreme value theorem.

Answer to Problem 9E

The minimum value exists at $x=a$ and maximum value exist at $x=c$ .

Also, the extreme value theorem doesn’t apply here as the function is not continuous.

Explanation of Solution

Given information:

The graph is:

  

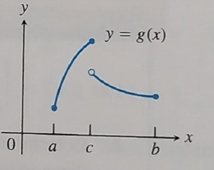
Concept Used:

The extreme values are the points where any x values minimum and maximum value of y is obtained.

Extreme value theorem: For any real valued function if it is continuous in a closed interval then it must attain a maximum and a minimum both at least once.

From the given graph it can be seen that the function is not continuous in a closed interval $\left[a,b\right]$ as the function is not continuous at c . So, extreme value theorem doesn’t apply.

While looking at the graph it can be concluded that the minimum value exists at $x=a$ and maximum value exist at $x=c$ .