Chapter 3, Problem 3.87QP

Interpretation Introduction

Interpretation:

3s, 3p and 3d orbitals which have the same energy in a hydrogen atom but different energies in a many-electron atom should be explained by using the concept of quantum numbers and Aufbau principle.

Concept Introduction:

Energies of orbitals in the hydrogen atom

The energies of orbitals in the hydrogen atom depend only on the value of the principal quantum number (n).  When n increases, energy also increases.  For this reason, orbitals in the same shell have the same energy in spite of their subshell.  The increasing order of energy of hydrogen orbitals is

1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f

In the case of one 2s and three 2p orbitals in the second shell, they have the same energy.  In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy.  All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.

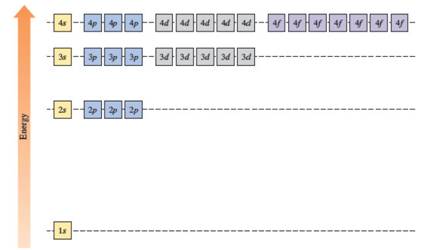
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram.  Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.

Energies of orbitals in a many electron atom

Energy of an orbital in a many electron atom depends on both the values of principle quantum number (n) and angular momentum quantum number (l).  For a given value of principle quantum number (n), the energy of orbital increases with increasing value of the angular momentum quantum number (l) in a many electron atom.

Principal Quantum Number (n)

The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron.  If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater.  Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom.  If all orbitals have the same value of ‘n’, they are said to be in the same shell (level).  The total number of orbitals for a given n value is n².  As the value of ‘n’ increases, the energy of the electron also increases.

Angular Momentum Quantum Number (l)

The angular momentum quantum number (l) explains the shape of the atomic orbital.  The values of l are integers which depend on the value of the principal quantum number, n.  For a given value of n, the possible values of l range are from 0 to n − 1.  If n = 1, there is only one possible value of l (l=0).  If n = 2, there are two values of l: 0 and 1.  If n = 3, there are three values of l: 0, 1, and 2.  The value of l is selected by the letters s, p, d, and f.  If l = 0, we have an s orbital; if l = 1, we have a p orbital; if l = 2, we have a d orbital and finally if l = 3, we have a f orbital.  A collection of orbitals with the same value of n is called a shell.  One or more orbitals with the same n and l values are referred to a subshell (sublevel).  The value of l also has a slight effect on the energy of the subshell; the energy of the subshell increases with l (s < p < d < f).

Aufbau principle

In the ground state of an atom, an electron enters the orbital with lowest energy first and subsequent electrons are fed in the order of increasing energies. This is called Aufbau principle.  The word 'aufbau' in German means 'building up'. Here, it refers to the filling up of orbitals with electrons.  Aufbau principle explains the theoretical, sequential building up of the stepwise addition of protons and electrons for the elements in the periodic table.