
(a)
To find:The domain of function.
(a)
Answer to Problem 52E
The domain of function is all the real numbers except x=0 .
Explanation of Solution
Given information:
The function is f(x)=1−x2x
Calculation:
Consider the function.
. f(x)=1−x2x
The function is valid for all the real numbers except x=0 as the denominator becomes zero and the function is undefined for this value.
Therefore, the domain of function is all the real numbers except x=0
(b)
To find:The intercepts.
(b)
Answer to Problem 52E
The y- intercept is absent and the x- intercept is (0,1) and (0,−1) .
Explanation of Solution
Given information:
The function is f(x)=1−x2x
Calculation:
The y intercept is absent as the function becomes undefined.
Equate function to zero to find x intercept.
f(0)=01−x2x=0x2=1x=±1
Therefore, the y- intercept is absent and the x- intercept is (0,1) and (0,−1) .
(c)
To find:The asymptotes.
(c)
Answer to Problem 52E
The slant asymptote is y=−x .
Explanation of Solution
Given information:
The function is f(x)=1−x2x
Calculation:
In given function degree of numerator is one more than the degree of denominator. The graph will have slant asymptote which can be calculated by dividing numerator wuth denominator.
f(x)=−x+1x
Here the slant asymptote will be y=−x as 1x becomes zero when x becomes infinite.
Therefore, the slant asymptote is y=−x .
(d)
To find:The sketch of graph.
(d)
Answer to Problem 52E
The graph is shown in Figure-(1).
Explanation of Solution
Given information:
The function is f(x)=1−x2x
Calculation:
The below table shows additional points
| Test Interval | Value of x | Value of f | Sign | Point of f |
| (−∞,−1) | -2 | 32 | Positive | (−2,32) |
| (−,0) | −12 | −32 | Negative | (−12,−32) |
| (0,1) | 12 | 32 | Positive | (12,32) |
| (1,∞) | 2 | −32 | Negative | (2,−32) |
Draw the sketch for the function by using the equations of asymptotes.
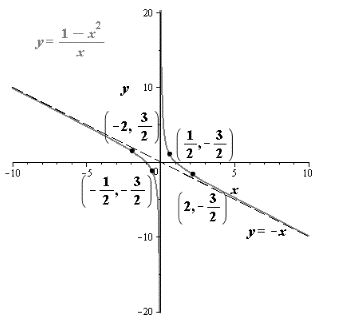
Figure-(1)
Therefore, the graph is shown in Figure-(1).
Chapter 2 Solutions
Precalculus with Limits
- quick solve thisarrow_forwardquick solve thisarrow_forwardThis table displays the current in equal intervals. Time t/ms 05 10 15 20 25 30 Current i/A 0 4.8 9.1 12.7 8.8 3.5 0 The formula for the charge as follows: 30x10-3 q 0 i dt Use formula to solve the current at 30ms using both the trapezoidal rule and Simpson's rule showing all steps and workingarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





