Chapter 2.2, Problem 115E

(a)

To determine

To sketch : The graph of the function $f\left(x\right)=x^4$ and explain how the graph of function $g$ differs from the graph of $f$ and determine when $g$ is even, odd or neither.

Explanation of Solution

Given: The function is $g\left(x\right)=f\left(x\right)+2$

The graph of $f\left(x\right)=x^4$ is shown in figure below.

  

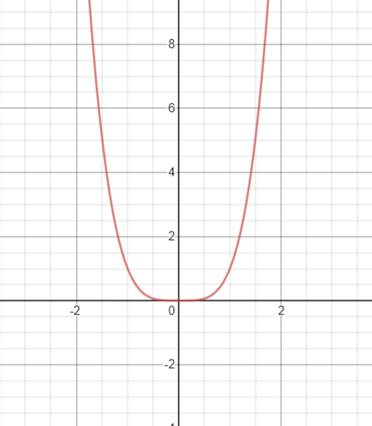
Figure (1)

Consider the function $g$ .

  $g\left(x\right)=f\left(x\right)+2$

The graph of $g$ shifts up by $2$ units.

The function is symmetric about the $y$ axis. So, the function is even.

Therefore, the graph of the function $f\left(x\right)$ is shown in figure (1), the function $g$ shifts up $2$ units with respect to the graph of $f\left(x\right)$ and the function is even.

(b)

To determine

To explain : How the graph of function $g$ differs from the graph of $f$ and determine when $g$ is even, odd or neither.

Explanation of Solution

Given: The function is $g\left(x\right)=f\left(x+2\right)$

Consider the function $g$ .

  $g\left(x\right)=f\left(x\right)+2$

The graph of $g$ shifts left by $2$ units.

The graph is shown in figure below.

  

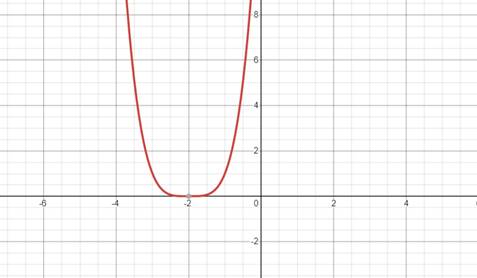
Figure (2)

The function is neither symmetric about the $y$ axis and neither to the origin So, the function is neither even nor odd.

Therefore, the function $g$ shifts left $2$ units with respect to the graph of $f\left(x\right)$ and the function is even.

(c)

To determine

To explain : How the graph of function $g$ differs from the graph of $f$ and determine when $g$ is even, odd or neither.

Explanation of Solution

Given: The function is $g\left(x\right)=f\left(-x\right)$

Consider the function $g$ .

  $g\left(x\right)=f\left(-x\right)$

The graph remains the same

The graph is shown in figure below.

  

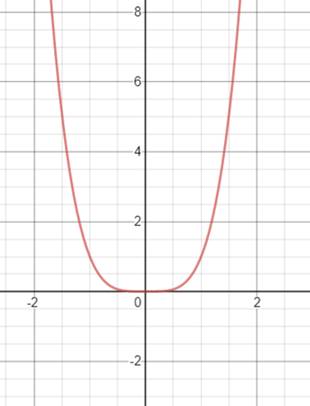
Figure (2)

The function is symmetric about the origin. So, the function is odd.

Therefore, the function $g$ remains same to the graph of $f\left(x\right)$ and the function is odd.

(d)

To determine

To explain : How the graph of function $g$ differs from the graph of $f$ and determine when $g$ is even, odd or neither.

Explanation of Solution

Given: The function is $g\left(x\right)=-f\left(x\right)$

Consider the function $g$ .

  $g\left(x\right)=-f\left(x\right)$

The graph is the reflection of $f\left(x\right)$ over the $x$ axis.

The graph is shown in figure below.

  

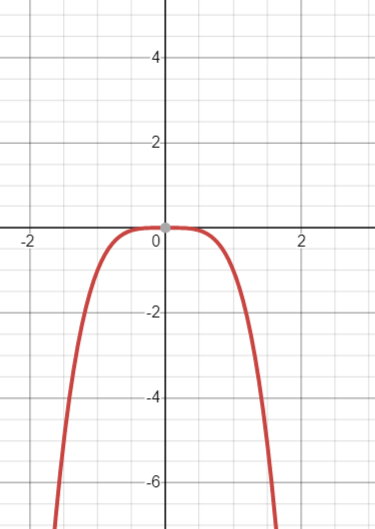
Figure (4)

The function is symmetric about the origin. So, the function is odd.

Therefore, the function $g$ is the reflection to the graph of $f\left(x\right)$ and the function is odd.

(e)

To determine

To explain : How the graph of function $g$ differs from the graph of $f$ and determine when $g$ is even, odd or neither.

Explanation of Solution

Given: The function is $g\left(x\right)=f\left(\frac{1}{2}\right)$

Consider the function $g$ .

  $g\left(x\right)=f\left(\frac{1}{2}\right)$

The graph has horizontal stretch by $2$ unit.

The graph is shown in figure below.

  

Figure (5)

The function is symmetric about the y axis. So, the function is even.

Therefore, the function $g$ has the horizontal stretch of $2$ to the graph of $f\left(x\right)$ and the function is even.

(f)

To determine

To explain : How the graph of function $g$ differs from the graph of $f$ and determine when $g$ is even, odd or neither.

Explanation of Solution

Given: The function is $g\left(x\right)=\frac{1}{2}f\left(x\right)$

Consider the function $g$ .

  $g\left(x\right)=\frac{1}{2}f\left(x\right)$

The graph has vertical shrink by $2$ unit.

The graph is shown in figure below.

  

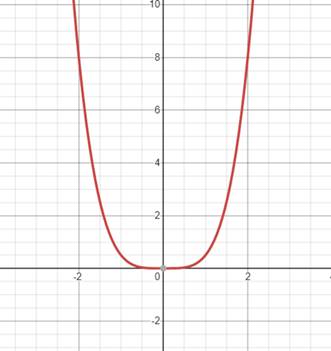
Figure (6)

The function is symmetric about the y axis. So, the function is even.

Therefore, the function $g$ has the vertical shrink of $2$ to the graph of $f\left(x\right)$ and the function is even.

(g)

To determine

To explain : How the graph of function $g$ differs from the graph of $f$ and determine when $g$ is even, odd or neither.

Explanation of Solution

Given: The function is $g\left(x\right)=f\left(x^{3/4}\right)$

Consider the function $g$ .

  $g\left(x\right)=f\left(x^{3/4}\right)$

The graph is a third degree polynomial whose domain is the set of non-negative real number.

The graph is shown in figure below.

  

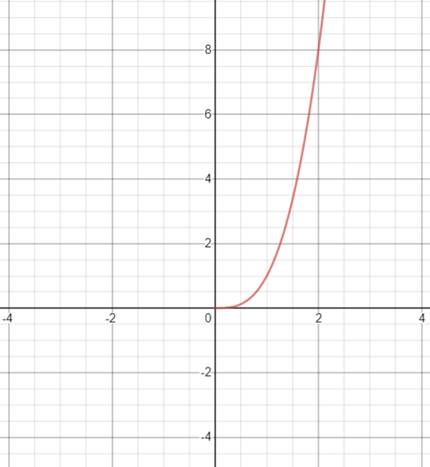
Figure (7)

The function is neither symmetric about the y axis not the origin. So, the function is neither.

Therefore, the function $g$ is a degree polynomial whose domain is the set of non-negative real number and the function is neither.

(h)

To determine

To explain : How the graph of function $g$ differs from the graph of $f$ and determine when $g$ is even, odd or neither.

Explanation of Solution

Given: The function is $g\left(x\right)=\left(f\circ f\right)\left(x\right)$

Consider the function $g$ .

  $g\left(x\right)=\left(f\circ f\right)\left(x\right)$

The graph is a sixteenth degree polynomial.

The graph is shown in figure below.

  

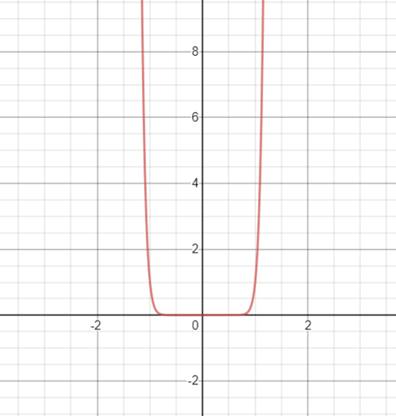
Figure (8)

The function is symmetric about the y axis. So, the function is even.

Therefore, the function $g$ is a sixteenth degree polynomial and the function is even.