Chapter 2.5, Problem 72E

To determine

To write : the polynomial as the product of linear factors and list all the zeros of function

Answer to Problem 72E

The function as product of linear factors: $\boxed{\boxed{f\left(x\right)=\left(x+3\right)\left(x-2-3i\right)\left(x-2+3i\right)}}$

The zeros of the function are: $\boxed{\boxed{x=-3;2+3i;2-3i}}$

Explanation of Solution

Given information: $f\left(x\right)=x^3-x^2+x+39$

Concept Involved:

Linear Factorization Theorem:If $f\left(x\right)$ is a polynomial of degree $n$ , where $n>0$ , then $f\left(x\right)$ has precisely $n$ linearfactors $f\left(x\right)=a_n\left(x-c_1\right)\left(x-c_2\right)...\left(x-c_n\right)$ where $c_1,c_2,...,c_n$ are complex numbers.

Complex Zeros Occur in Conjugate Pairs: Let f be a polynomial function that has real coefficients. If $a+bi$ , where $b\ne 0$ , is a zero of the function, then the complex conjugates $a-bi$ is alsoa zero of the function.

Synthetic Division (for a Cubic Polynomial):To divide $a{x}^3+b{x}^2+cx+d$ by $x-k$ , use this pattern.

$\begin{array}{l}\begin{array}{l}k\\ \end{array}|\stackrel{Coefficientofdividend}{\overbrace{\underset{\_}{\begin{array}{cccc}\boxed{a}& b& c& d\\ \downarrow & \underset{\downarrow }{\boxed{ka}}& \underset{\downarrow }{\boxed{}}& \underset{\downarrow }{\boxed{}}\end{array}}}}\\ \begin{array}{ccccc}& \nearrow & \nearrow & \nearrow & \end{array}\\ \underset{Coefficientofquotient}{\underbrace{\begin{array}{ccc}\boxed{a}& \boxed{}& \boxed{}\end{array}}}\begin{array}{cc}\boxed{r}& \leftarrow \text{Remainder}\end{array}\end{array}$

In case when we have a polynomial with a missing term, insert placeholders with zero coefficients for missing powers of the variable. Vertical pattern: Add terms in columns Diagonal pattern: Multiply results by k. This algorithm for synthetic division works only for divisors of the form x - k. Remember that $x+k=x-\left(-k\right)$ .

The Division Algorithm: If $f\left(x\right)$  and   $d\left(x\right)$ are polynomials such that $d\left(x\right)\ne 0$ , and the degree of $d\left(x\right)$ isless than or equal to the degree of $f\left(x\right)$ , then there exist unique polynomials $q\left(x\right)$  and   $r\left(x\right)$ such that $\underset{\stackrel{\uparrow }{{\displaystyle Dividend}}}{{\displaystyle \text{f (x)}}}\text{ = }\underset{\stackrel{\uparrow }{{\displaystyle Divisor}}}{{\displaystyle \text{d(x)}}}\cdot \underset{\stackrel{\uparrow }{{\displaystyle Quotient}}}{{\displaystyle \text{q(x)}}}+\underset{\stackrel{\uparrow }{{\displaystyle Remainder}}}{{\displaystyle \text{ r (x)}}}$ where $r\left(x\right)=0$ or the degree of $r\left(x\right)$ is less than the degree of $d\left(x\right)$ . If theremainder $r\left(x\right)$ is zero, then $d\left(x\right)$ divides evenly into $f\left(x\right)$ and k can be called as zero of the polynomial.

Graph:

  

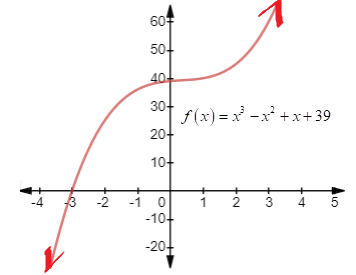
Interpretation:

From the graph of the function we can pick possible zeros of the function as $x=-3$ and check using synthetic division whether they are actual zeros.

Calculation:

Use synthetic division to find the other zeros of the function

  $\begin{array}{l}\begin{array}{l}-3\\ \end{array}|\underset{\_}{\begin{array}{c}1\\ \end{array}\begin{array}{c}-1\\ -3\end{array}\begin{array}{c}1\\ 12\end{array}\begin{array}{c}39\\ -39\end{array}}\\ 1-413\overline{)0}\leftarrow Remainder\end{array}$

If $k=-3$ is zero, then $x-k$ that is $x+3$ will be factor of the polynomial. The numbers in the last row make up your coefficients of the quotient as well as the remainder. The final value on the right is the remainder. Working right to left, the next number is your constant, the next is the coefficient for x , the next is the coefficient for x squared, and so on.

  $\left(x^3-x^2+x+39\right)÷\left(x+3\right)=\stackrel{Quotient}{\overbrace{x^2-4x+13}}$

To find other zeros of the polynomial $f\left(x\right)=x^3-x^2+x+39$ , set Quotient of synthetic division to zero and solve for x .

  $x^2-4x+13=0$

We can solve this equation using completing the square method by subtracting 5 on both sides of the equation

  $x^2-4x+13-13=0-13$

Simplify on both sides of the equation

  $x^2-4x=-13$

In order to make the left side expression as perfect square trinomial, we need to add square of half of coefficient of x on both sides

  $x^2-4x+{\left(4/2\right)}^2=-13+{\left(4/2\right)}^2$

Simplify on right side of the equation

  $x^2-4x+4=-9$

Write the left side as a perfect square

  ${\left(x-2\right)}^2=-9$

Rewrite the right side of the equation

  ${\left(x-2\right)}^2=-1\cdot 9$

Take square root on both sides

  $\sqrt{{\left(x-2\right)}^2}=\sqrt{-1}\cdot \sqrt{9}$

Simplifying square root on both sides of the equation

  $x-2=\pm 3\cdot \sqrt{-1}$

Replace $i$ for $\sqrt{-1}$

  $x-2=\pm 3i$

Add 2 on both sides of the equation

  $x-2+2=2\pm 3i$

Simplify in left side of the equation

  $x=2\pm 3i$

List the zeros of the functions given:

  $x=-3\left\{Fromgraph\right\};x=2+i;x=2-i$

If $x=k$ is zero, then $x-k$ will be the factor of the function.

So $x+3,x-\left(2+3i\right)$ & $x-\left(2-3i\right)$ are the factors of the function

Write the function $f\left(x\right)=x^3-x^2+x+39$ as product of linear factors:

  $f\left(x\right)=\left(x+3\right)\left(x-2-3i\right)\left(x-2+3i\right)$

Conclusion:

The zeros of the given function $f\left(x\right)=x^3-x^2+x+39$ are: $x=-3;2+3i;2-3i$

The function written as product of linear factors: $f\left(x\right)=\left(x+3\right)\left(x-2-3i\right)\left(x-2+3i\right)$