Chapter 10.4, Problem 30AYU

In Problems 29-36, find the center, transverse axis, vertices, foci, and asymptotes. Graph each equation by hand. Verify your graph using a graphing utility.

$\frac{y^2}{16}-\frac{x^2}{4}=1$

To determine

a.

To find: Center, transverse axis, vertices, foci and asymptotes.

Answer to Problem 30AYU

Solution:

Center: $\left(0,0\right)$.

The transverse axis is $y\text{-axis}$.

Vertex: $\left(0,4\right),\left(0,-4\right)$.

Foci: $\left(0,2\surd 5\right)$, $\left(0,-2\surd 5\right)$.

Asymptotes: $y=2x$, $y=-2x$.

Explanation of Solution

Given:

$\frac{y^2}{16}-\frac{x^2}{4}=1$

Formula used:

Center	Transverse axis	Foci	Vertices	Equation	Asymptotes
$\left(0,0\right)$	$y\text{-axis}$	$\left(0,\pm c\right)$	$\left(0,\pm a\right)$	$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$; $b^2=c^2-a^2$	$x=\pm \frac{a}{b}y$

Calculation:

Consider the given equation $\frac{y^2}{16}-\frac{x^2}{4}=1$.

The center of the hyperbola is $\left(0,0\right)$;

From the given data we see that, transverse axis is $y\text{-axis}$.

$a=4,b=2$, $c=\sqrt{b^2+a^2},c=\sqrt{16+4}=2\surd 5$

Vertex: $\left(0,\pm a\right)=\left(0,\pm 4\right)$.

Foci: $\left(0,\pm c\right)=\left(0,\pm 2\surd 5\right)$;

Asymptotes: $y=\pm \frac{a}{b}x=\pm \frac{4x}{2}=\pm 2x$.

b.

To graph:

The equation $\frac{y^2}{16}-\frac{x^2}{4}=1$.

Solution:

Given:

$\frac{y^2}{16}-\frac{x^2}{4}=1$

Graph:

The graph of the equation of $\frac{y^2}{16}-\frac{x^2}{4}=1$ is plotted.

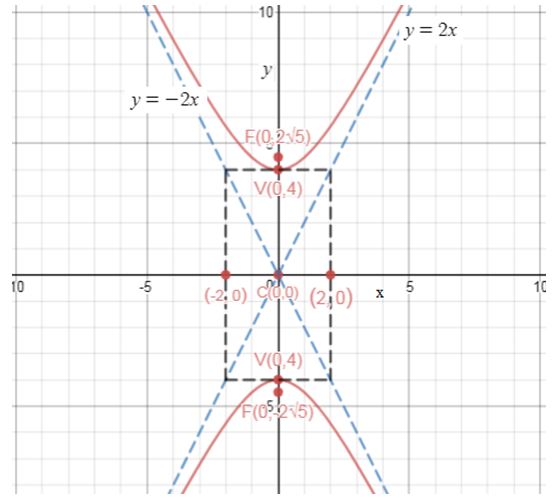
Using the given equation $\frac{y^2}{16}-\frac{x^2}{4}=1$. We find $a=4$, $b=2$. We have found the.

Center: $\left(0,0\right)$.

The transverse axis is $y\text{-axis}$.

Vertex: $\left(0,\pm 4\right)$.

Foci: $\left(0,\pm 2\surd 5\right)$;

Asymptotes: $y=\pm 2x$.