
Concept explainers
In Problems 21-38, find the equation of the parabola described. Find the two points that define the latus rectum, and graph the equation by hand.
Focus at ; vertex at
(a & b)
The equation of the parabola described and two points that define the latus rectum for the following description.
Focus at ; vertex at .
Answer to Problem 19AYU
, Latus rectum: and .
Explanation of Solution
Given:
Focus at ; vertex at .
Formula used:
| Vertex | Focus | Directrix | Equation | Description |
| Parabola, axis of symmetry is , opens right |
Calculation:
The vertex and focus both lie on the horizontal line (The axis of symmetry). The distance from the vertex to the focus is .
Also, because the focus lies to the right of the vertex, the parabola opens to the right.
; where . Therefore the equation is,
The equation of the parabola is .
To find the points that define the latus rectum, Let in the above equation.
We get,
Hence and defines the latus rectum.
c.
To graph: The parabola for the equation .
Answer to Problem 19AYU
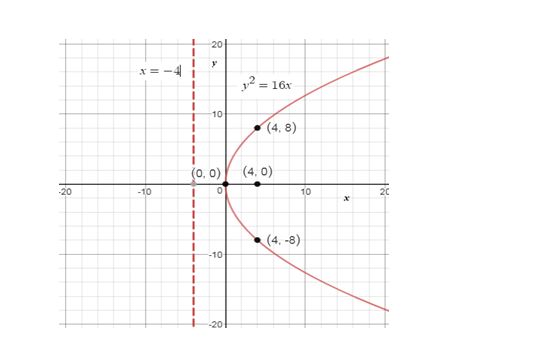
Explanation of Solution
Given:
Focus at ; vertex at .
Calculation:
Parabola is plotted for the equation .

Using the given information and we have formed the equation and plotted the graph for . The focus and the vertex lie on the horizontal line.
The equation for directrix D: is shown as dotted line. The parabola opens at the right. The points and define the latus rectum.
Chapter 10 Solutions
Precalculus Enhanced with Graphing Utilities
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
Algebra and Trigonometry (6th Edition)
College Algebra (7th Edition)
A First Course in Probability (10th Edition)
University Calculus: Early Transcendentals (4th Edition)
- Solve work shown please and thanks!arrow_forwardGiven the following graph of the function y = f(x) and n = = 6, answer the following questions about the area under the curve from x graph to enlarge it.) 1 (Round your answer to within two decimal places if necessary, but do not round until your final computation.) a. Use the Trapezoidal Rule to estimate the area. Estimate: T6 G b. Use Simpson's Rule to estimate the area. Estimate: S6 - ID = 0 to x = 6. (Click on aarrow_forward"Solve the following differential equation using the Operator Method and the Determinant Method:" Solve by dr no ai """'+3y"" + 3y+y=arrow_forward
- (4,4) M -4 2 2 -4 (-4,-4) 4 8 10 12 (8,-4) (12,-4) Graph of f The figure shows the graph of a piecewise-linear function f. For −4≤x≤12, the function g is x defined by g(x) = √ƒ (t)dt . . Find the value of g(6). Find the value of g'(6). |arrow_forwardPREVIOUS ANSWERS ASK YOUR TEACHER PRACTICE ANOTHER Find the derivative of the function. f'(x) = X x + √3x f(x) = 3x-5 (3√√3x+11√√x+5√3 2√√x (3x-5)² Need Help? Read It SUBMIT ANSWERarrow_forwardPREVIOUS ANSWERS ASK YOUR TEACHER PRACTICE A Find the derivative of the function and evaluate f'(x) at the given val f(x) = (√√√x + 3x) (x3/2 - x); x = 1 f'(x) = 9x 412 (12x (13) 2 - 4x-3√√√x f'(1) = 2 Need Help? Read It Watch It SUBMIT ANSWERarrow_forward
- Consider the following functions. g(x) = x + √3x h(x) = 3x-5 x + √3x f(x) = = 3x-5 Find the derivative of each function. g'(x) h'(x) = = f'(x) = 3 = +1 2√3x 3 (3√3x + 10√√x +5√√√3 2√√x (3x-5)² Need Help? Read It SUBMIT ANSWERarrow_forward"Solve the following differential equation using the Operator Method and the Determinant Method:" y'''' + 3y'"' + 3y'' + y = xarrow_forwardpractice for exam please helparrow_forward
- Fig. 4.22. Problems 4.1 (A). Determine the second moments of area about the axes XX for the sections shown in Fig. 4.23. [15.69, 7.88, 41.15, 24; all x 10-6 m. All dimensions in mm IAA inn 100 25 50 25 50 80 50 50 Fig. 4.23. X 80 60arrow_forward4.3 (A). A conveyor beam has the cross-section shown in Fig. 4.24 and it is subjected to a bending moment in the plane YY. Determine the maximum permissible bending moment which can be applied to the beam (a) for bottom flange in tension, and (b) for bottom flange in compression, if the safe stresses for the material in tension and compression are 30 MN/m² and 150 MN/m² respectively. Y [32.3, 84.8 kNm.] 150 100 50 -25 +50-50-50-50- All dimensions in mmarrow_forward"Find the values of V1, V2, and V3 by solving the following differential equation system:" 1 L1 1 X - X x 2 - 2x x2 x3 x² - 4x + 2] M Larrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





